Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 10612 by FilupS last updated on 20/Feb/17

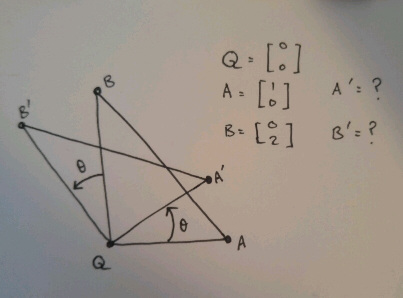
Commented by FilupS last updated on 20/Feb/17

Solve for A′ and B′ via: 1. Vectors 2. Triganometry

$$\mathrm{Solve}\:\mathrm{for}\:\boldsymbol{{A}}'\:\mathrm{and}\:\boldsymbol{{B}}'\:\mathrm{via}: \\ $$$$\mathrm{1}.\:\:\mathrm{Vectors} \\ $$$$\mathrm{2}.\:\:\mathrm{Triganometry} \\ $$

Answered by sandy_suhendra last updated on 20/Feb/17

by trigonometry QA=QA′=(√(1^2 +0^2 ))=1 x_(A′) = 1 cos θ = cos θ y_(A′) = 1 sin θ = sin θ so A′ = [((cos θ)),((sin θ)) ] QB=QB′ = (√(0^2 +2^2 )) = 2 x_(B′) = 2 cos (90°+θ) = −2 sin θ y_(B′) = 2 sin (90°+θ) = 2 cos θ so B′ = [((−2 sin θ)),(( 2 cos θ)) ]

$$\mathrm{by}\:\mathrm{trigonometry} \\ $$$$\mathrm{QA}=\mathrm{QA}'=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{x}_{\mathrm{A}'} \:=\:\mathrm{1}\:\mathrm{cos}\:\theta\:=\:\mathrm{cos}\:\theta \\ $$$$\mathrm{y}_{\mathrm{A}'} \:=\:\mathrm{1}\:\mathrm{sin}\:\theta\:=\:\mathrm{sin}\:\theta \\ $$$$\mathrm{so}\:\mathrm{A}'\:=\:\begin{bmatrix}{\mathrm{cos}\:\theta}\\{\mathrm{sin}\:\theta}\end{bmatrix} \\ $$$$\mathrm{QB}=\mathrm{QB}'\:=\:\sqrt{\mathrm{0}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:=\:\mathrm{2} \\ $$$$\mathrm{x}_{\mathrm{B}'} \:=\:\mathrm{2}\:\mathrm{cos}\:\left(\mathrm{90}°+\theta\right)\:=\:−\mathrm{2}\:\mathrm{sin}\:\theta \\ $$$$\mathrm{y}_{\mathrm{B}'} \:=\:\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{90}°+\theta\right)\:=\:\mathrm{2}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{so}\:\mathrm{B}'\:=\:\begin{bmatrix}{−\mathrm{2}\:\mathrm{sin}\:\theta}\\{\:\:\:\mathrm{2}\:\mathrm{cos}\:\theta}\end{bmatrix} \\ $$

Answered by mrW1 last updated on 21/Feb/17

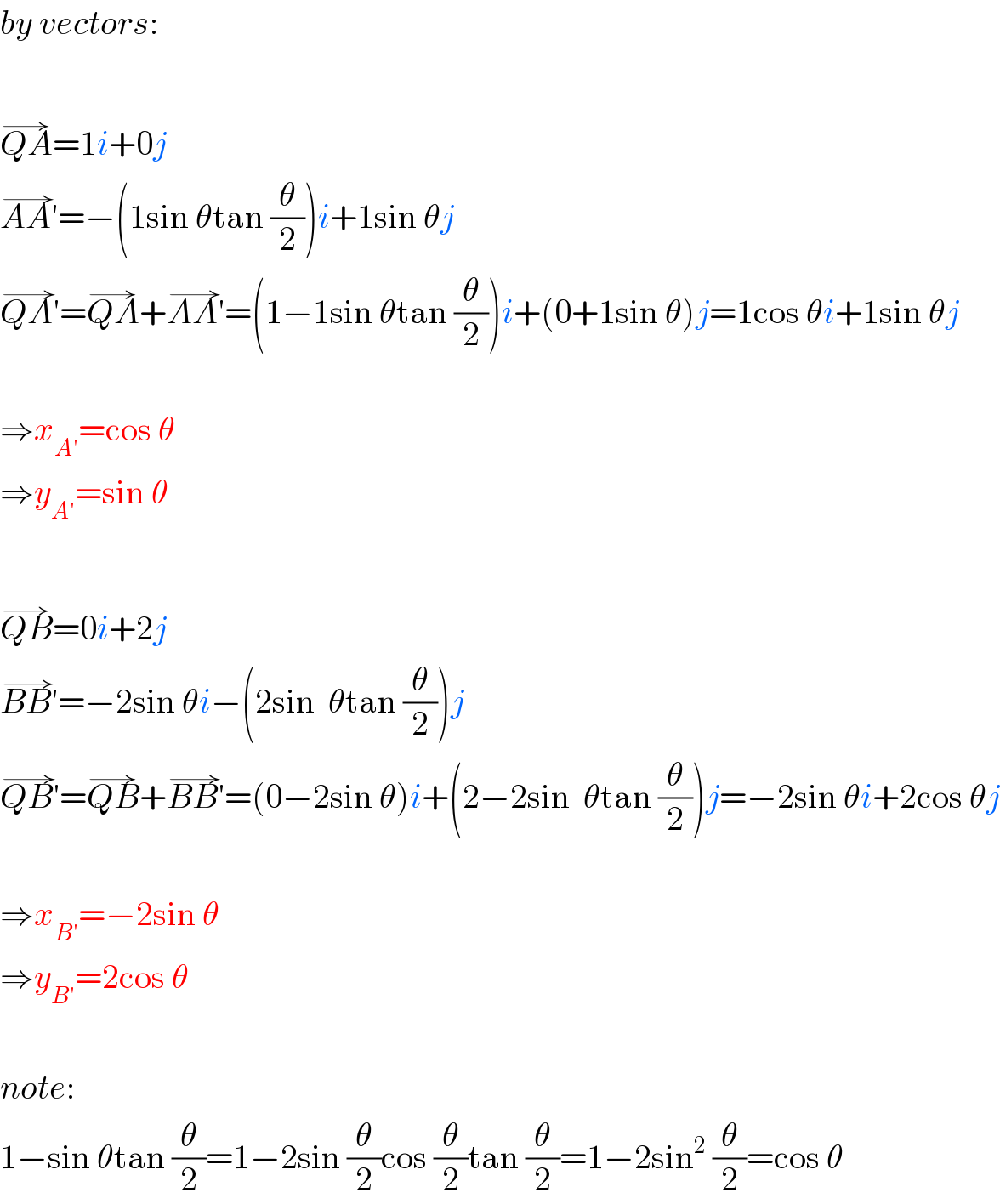
by vectors: QA^(→) =1i+0j AA′^(→) =−(1sin θtan (θ/2))i+1sin θj QA′^(→) =QA^(→) +AA′^(→) =(1−1sin θtan (θ/2))i+(0+1sin θ)j=1cos θi+1sin θj ⇒x_(A′) =cos θ ⇒y_(A′) =sin θ QB^(→) =0i+2j BB′^(→) =−2sin θi−(2sin θtan (θ/2))j QB′^(→) =QB^(→) +BB′^(→) =(0−2sin θ)i+(2−2sin θtan (θ/2))j=−2sin θi+2cos θj ⇒x_(B′) =−2sin θ ⇒y_(B′) =2cos θ note: 1−sin θtan (θ/2)=1−2sin (θ/2)cos (θ/2)tan (θ/2)=1−2sin^2 (θ/2)=cos θ

$${by}\:{vectors}: \\ $$$$ \\ $$$$\overset{\rightarrow} {{QA}}=\mathrm{1}{i}+\mathrm{0}{j} \\ $$$$\overset{\rightarrow} {{AA}'}=−\left(\mathrm{1sin}\:\theta\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right){i}+\mathrm{1sin}\:\theta{j} \\ $$$$\overset{\rightarrow} {{QA}'}=\overset{\rightarrow} {{QA}}+\overset{\rightarrow} {{AA}'}=\left(\mathrm{1}−\mathrm{1sin}\:\theta\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right){i}+\left(\mathrm{0}+\mathrm{1sin}\:\theta\right){j}=\mathrm{1cos}\:\theta{i}+\mathrm{1sin}\:\theta{j} \\ $$$$ \\ $$$$\Rightarrow{x}_{{A}'} =\mathrm{cos}\:\theta \\ $$$$\Rightarrow{y}_{{A}'} =\mathrm{sin}\:\theta \\ $$$$ \\ $$$$\overset{\rightarrow} {{QB}}=\mathrm{0}{i}+\mathrm{2}{j} \\ $$$$\overset{\rightarrow} {{BB}'}=−\mathrm{2sin}\:\theta{i}−\left(\mathrm{2sin}\:\:\theta\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right){j} \\ $$$$\overset{\rightarrow} {{QB}'}=\overset{\rightarrow} {{QB}}+\overset{\rightarrow} {{BB}'}=\left(\mathrm{0}−\mathrm{2sin}\:\theta\right){i}+\left(\mathrm{2}−\mathrm{2sin}\:\:\theta\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right){j}=−\mathrm{2sin}\:\theta{i}+\mathrm{2cos}\:\theta{j} \\ $$$$ \\ $$$$\Rightarrow{x}_{{B}'} =−\mathrm{2sin}\:\theta \\ $$$$\Rightarrow{y}_{{B}'} =\mathrm{2cos}\:\theta \\ $$$$ \\ $$$${note}: \\ $$$$\mathrm{1}−\mathrm{sin}\:\theta\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\mathrm{1}−\mathrm{2sin}\:\frac{\theta}{\mathrm{2}}\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}=\mathrm{cos}\:\theta \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com