
Question Number 105929 by Study last updated on 01/Aug/20
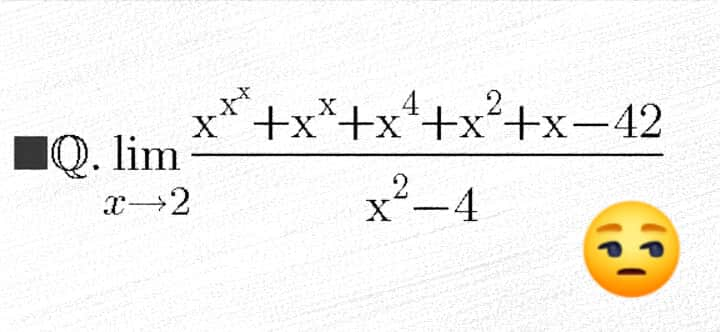
Answered by Dwaipayan Shikari last updated on 01/Aug/20
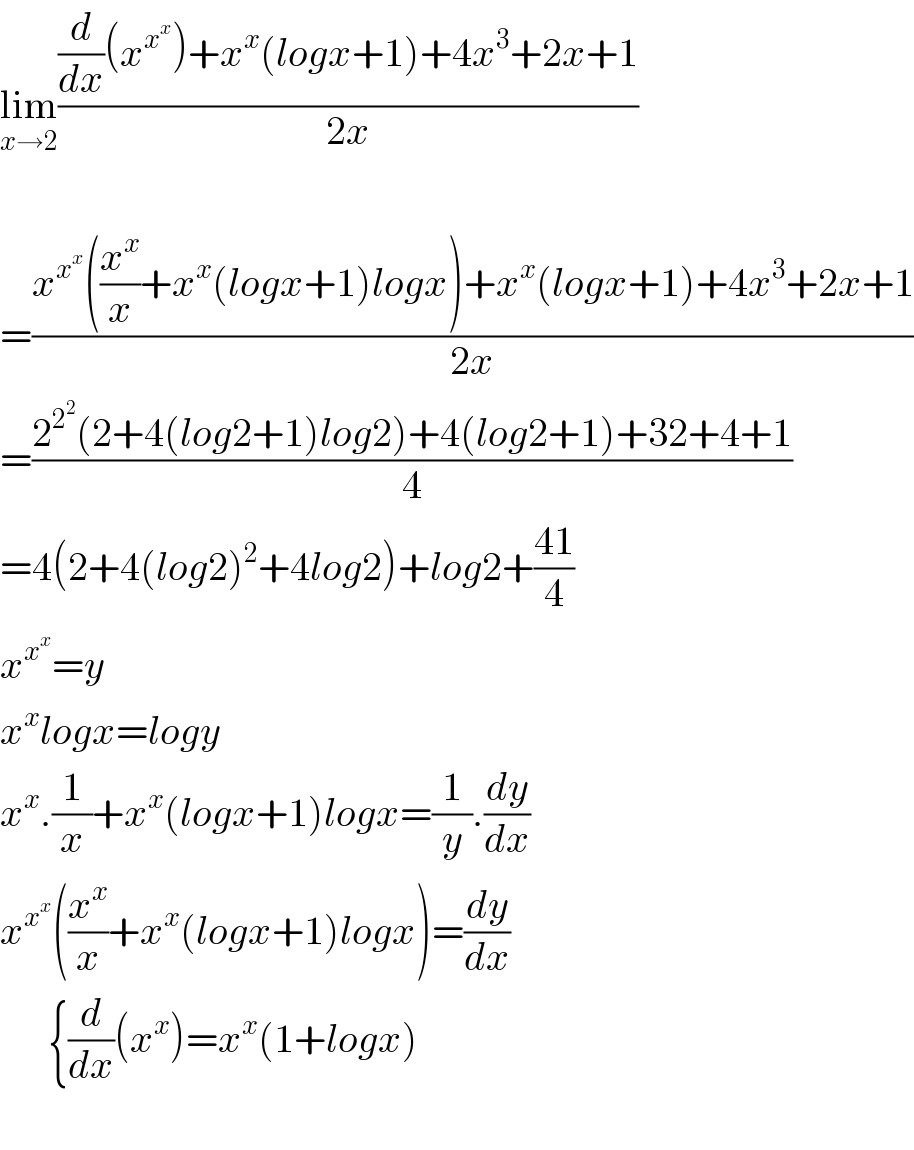
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left({x}^{{x}^{{x}} } \right)+{x}^{{x}} \left({logx}+\mathrm{1}\right)+\mathrm{4}{x}^{\mathrm{3}} +\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}{x}} \\ $$$$ \\ $$$$=\frac{{x}^{{x}^{{x}} } \left(\frac{{x}^{{x}} }{{x}}+{x}^{{x}} \left({logx}+\mathrm{1}\right){logx}\right)+{x}^{{x}} \left({logx}+\mathrm{1}\right)+\mathrm{4}{x}^{\mathrm{3}} +\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}{x}} \\ $$$$=\frac{\mathrm{2}^{\mathrm{2}^{\mathrm{2}} } \left(\mathrm{2}+\mathrm{4}\left({log}\mathrm{2}+\mathrm{1}\right){log}\mathrm{2}\right)+\mathrm{4}\left({log}\mathrm{2}+\mathrm{1}\right)+\mathrm{32}+\mathrm{4}+\mathrm{1}}{\mathrm{4}} \\ $$$$=\mathrm{4}\left(\mathrm{2}+\mathrm{4}\left({log}\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4}{log}\mathrm{2}\right)+{log}\mathrm{2}+\frac{\mathrm{41}}{\mathrm{4}} \\ $$$${x}^{{x}^{{x}} } ={y} \\ $$$${x}^{{x}} {logx}={logy} \\ $$$${x}^{{x}} .\frac{\mathrm{1}}{{x}}+{x}^{{x}} \left({logx}+\mathrm{1}\right){logx}=\frac{\mathrm{1}}{{y}}.\frac{{dy}}{{dx}} \\ $$$${x}^{{x}^{{x}} } \left(\frac{{x}^{{x}} }{{x}}+{x}^{{x}} \left({logx}+\mathrm{1}\right){logx}\right)=\frac{{dy}}{{dx}} \\ $$$$\:\:\:\:\:\:\left\{\frac{{d}}{{dx}}\left({x}^{{x}} \right)={x}^{{x}} \left(\mathrm{1}+{logx}\right)\right. \\ $$$$ \\ $$
