
Question Number 105113 by yahyajan last updated on 26/Jul/20
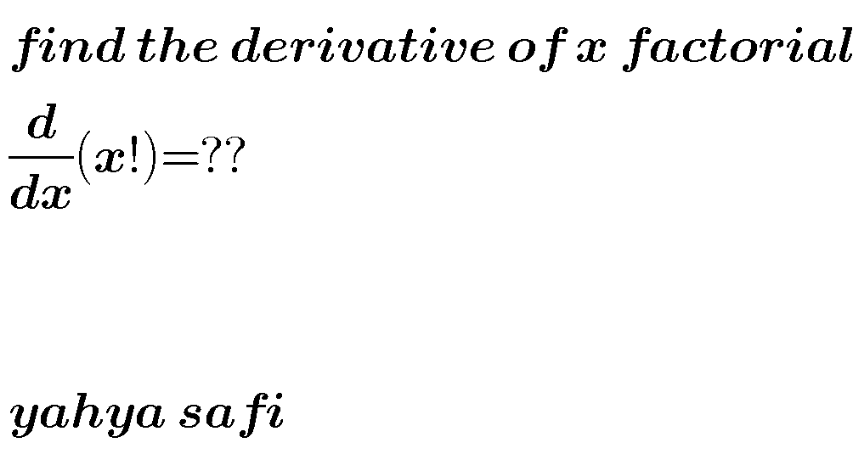
Answered by Dwaipayan Shikari last updated on 26/Jul/20
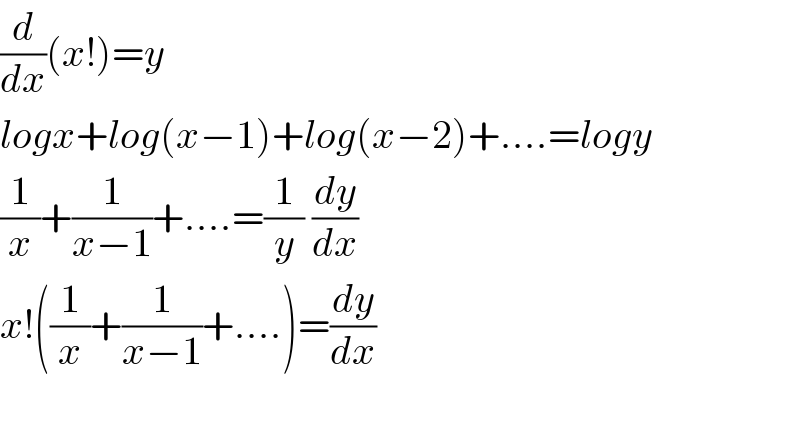
$$\frac{{d}}{{dx}}\left({x}!\right)={y} \\ $$$${logx}+{log}\left({x}−\mathrm{1}\right)+{log}\left({x}−\mathrm{2}\right)+....={logy} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}−\mathrm{1}}+....=\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}} \\ $$$${x}!\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}−\mathrm{1}}+....\right)=\frac{{dy}}{{dx}} \\ $$$$ \\ $$
Answered by OlafThorendsen last updated on 26/Jul/20
![x! = Γ(x+1) (d/dx)x! = Γ′(x+1) = Γ(x+1)ψ_0 (x+1) with by definition Γ(x+1) = xΓ(x) and ψ_0 (x+1) = ψ_0 (x)+(1/x) (d/dx)x! = xΓ(x)[ψ_0 (x)+(1/x)] (d/dx)x! = Γ(x)[xψ_0 (x)+1] Γ : Gamma function ψ_0 : digamma function (d/dx)x! = x!ψ_0 (x)+(x−1)!](Q105127.png)
$${x}!\:=\:\Gamma\left({x}+\mathrm{1}\right) \\ $$$$\frac{{d}}{{dx}}{x}!\:=\:\Gamma'\left({x}+\mathrm{1}\right)\:=\:\Gamma\left({x}+\mathrm{1}\right)\psi_{\mathrm{0}} \left({x}+\mathrm{1}\right) \\ $$$$\mathrm{with}\:\mathrm{by}\:\mathrm{definition}\:\Gamma\left({x}+\mathrm{1}\right)\:=\:{x}\Gamma\left({x}\right) \\ $$$$\mathrm{and}\:\psi_{\mathrm{0}} \left({x}+\mathrm{1}\right)\:=\:\psi_{\mathrm{0}} \left({x}\right)+\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{d}}{{dx}}{x}!\:=\:{x}\Gamma\left({x}\right)\left[\psi_{\mathrm{0}} \left({x}\right)+\frac{\mathrm{1}}{{x}}\right] \\ $$$$\frac{{d}}{{dx}}{x}!\:=\:\Gamma\left({x}\right)\left[{x}\psi_{\mathrm{0}} \left({x}\right)+\mathrm{1}\right] \\ $$$$\Gamma\::\:\mathrm{Gamma}\:\mathrm{function} \\ $$$$\psi_{\mathrm{0}} \::\:\mathrm{digamma}\:\mathrm{function} \\ $$$$\frac{{d}}{{dx}}{x}!\:=\:{x}!\psi_{\mathrm{0}} \left({x}\right)+\left({x}−\mathrm{1}\right)! \\ $$$$ \\ $$
