
Question Number 105076 by ajfour last updated on 25/Jul/20
Commented by ajfour last updated on 26/Jul/20

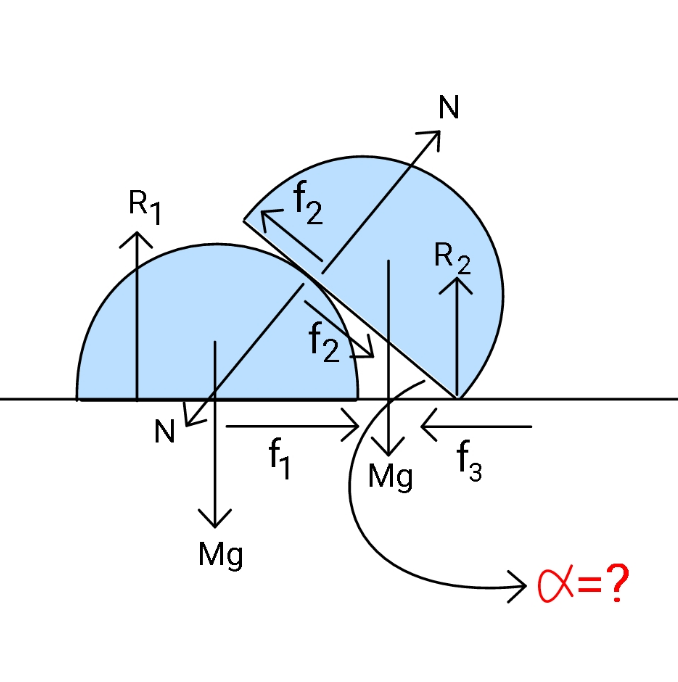
$${Let}\:{friction}\:{coefficient}\:{between} \\ $$$${ground}\:{and}\:{both}\:{semi}-{cylinders} \\ $$$${be}\:\boldsymbol{\mu}\:{given}.\:{Find}\:\alpha\:{and}\:{friction} \\ $$$${coefficient}\:{between}\:{both}\:{semi}- \\ $$$${cylindrical}\:{surfaces}\:\left(\eta\right)\:{if}\:{both} \\ $$$${semi}-{cylinders}\:{are}\:{on}\:{the}\:{verge} \\ $$$${of}\:{slipping}. \\ $$
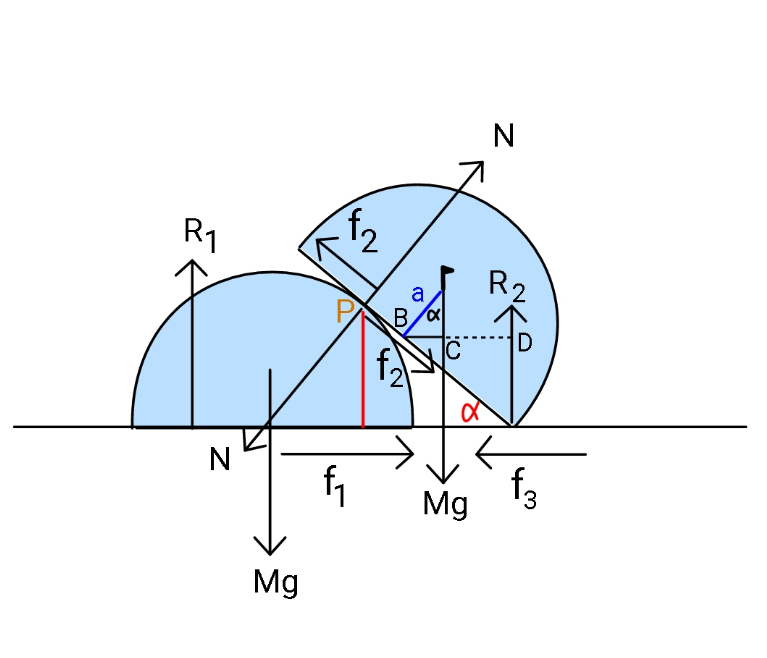
Answered by ajfour last updated on 26/Jul/20
Answered by mr W last updated on 26/Jul/20
Commented by ajfour last updated on 27/Jul/20
$${but}\:{i}\:{have}\:{edited}\:{the}\:{question}, \\ $$$${Sir}... \\ $$
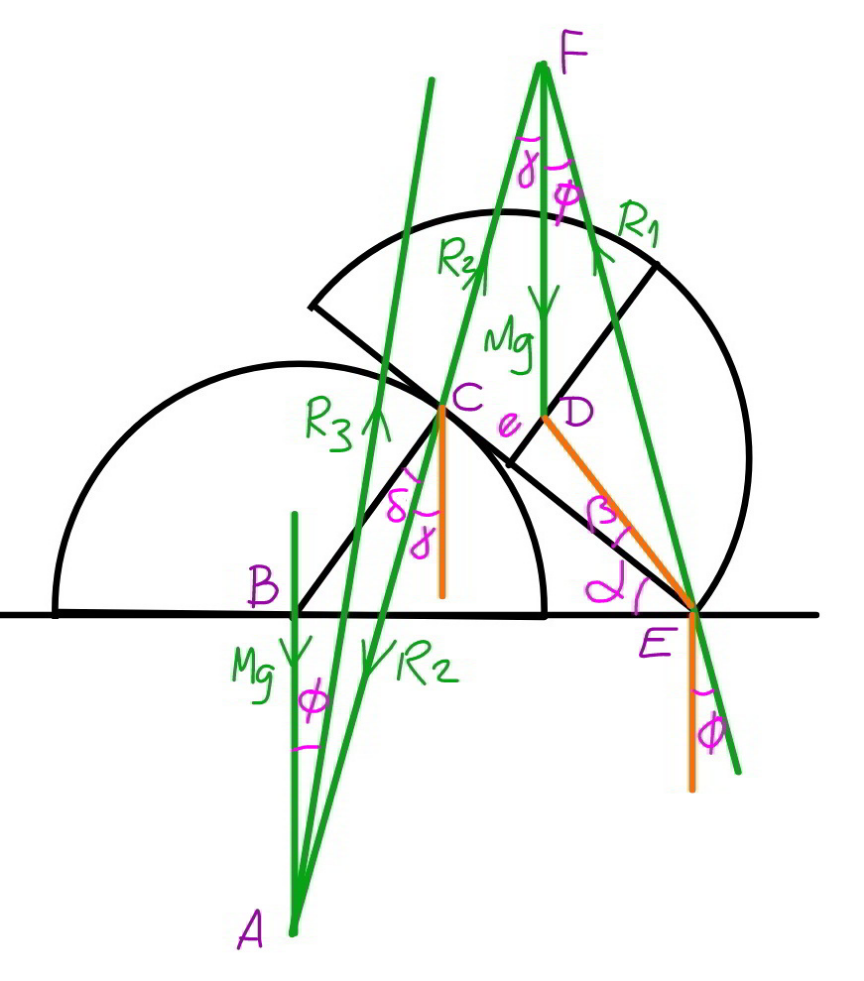
Commented by mr W last updated on 26/Jul/20
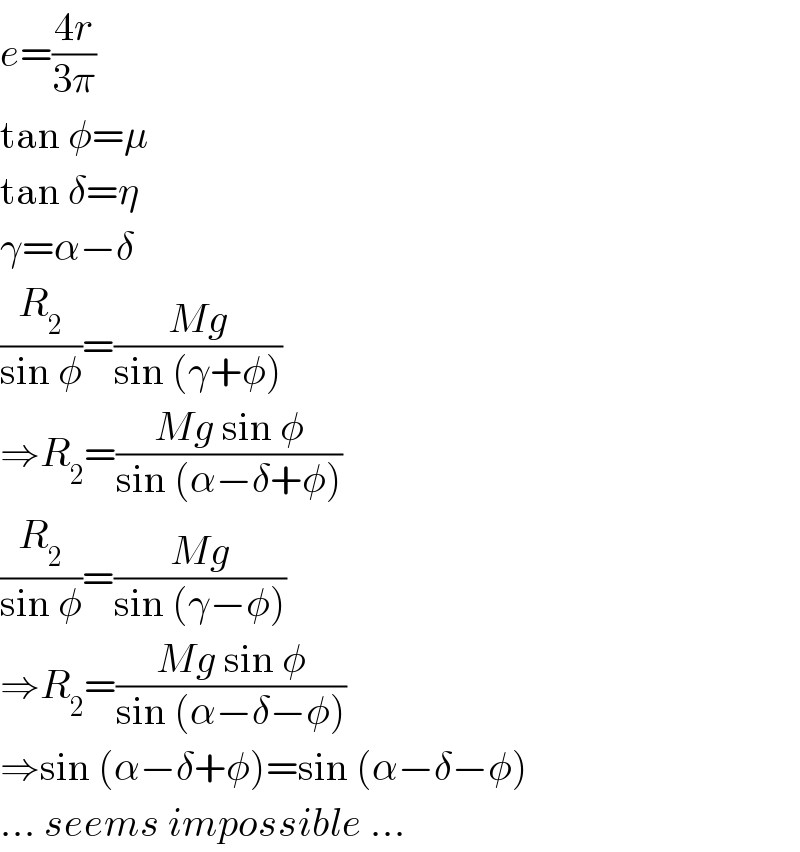
$${e}=\frac{\mathrm{4}{r}}{\mathrm{3}\pi} \\ $$$$\mathrm{tan}\:\phi=\mu \\ $$$$\mathrm{tan}\:\delta=\eta \\ $$$$\gamma=\alpha−\delta \\ $$$$\frac{{R}_{\mathrm{2}} }{\mathrm{sin}\:\phi}=\frac{{Mg}}{\mathrm{sin}\:\left(\gamma+\phi\right)} \\ $$$$\Rightarrow{R}_{\mathrm{2}} =\frac{{Mg}\:\mathrm{sin}\:\phi}{\mathrm{sin}\:\left(\alpha−\delta+\phi\right)} \\ $$$$\frac{{R}_{\mathrm{2}} }{\mathrm{sin}\:\phi}=\frac{{Mg}}{\mathrm{sin}\:\left(\gamma−\phi\right)} \\ $$$$\Rightarrow{R}_{\mathrm{2}} =\frac{{Mg}\:\mathrm{sin}\:\phi}{\mathrm{sin}\:\left(\alpha−\delta−\phi\right)} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\alpha−\delta+\phi\right)=\mathrm{sin}\:\left(\alpha−\delta−\phi\right) \\ $$$$...\:{seems}\:{impossible}\:... \\ $$
