
Question Number 101568 by Quvonchbek last updated on 03/Jul/20
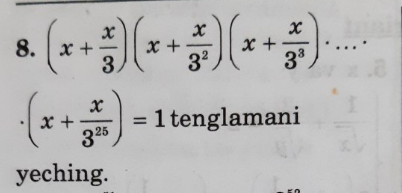
Answered by mr W last updated on 03/Jul/20
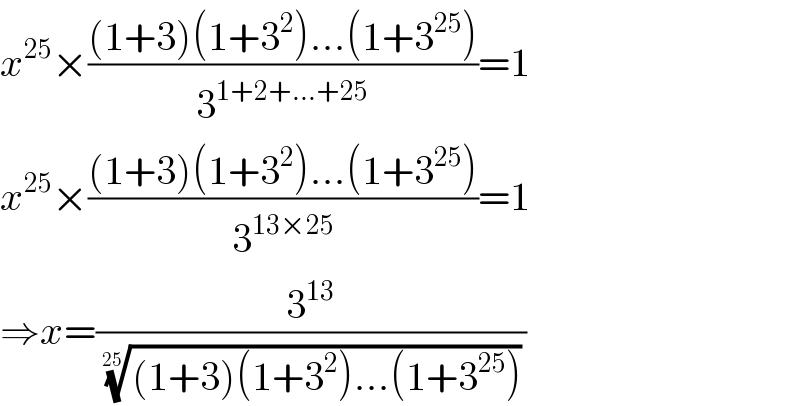
$${x}^{\mathrm{25}} ×\frac{\left(\mathrm{1}+\mathrm{3}\right)\left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} \right)...\left(\mathrm{1}+\mathrm{3}^{\mathrm{25}} \right)}{\mathrm{3}^{\mathrm{1}+\mathrm{2}+...+\mathrm{25}} }=\mathrm{1} \\ $$$${x}^{\mathrm{25}} ×\frac{\left(\mathrm{1}+\mathrm{3}\right)\left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} \right)...\left(\mathrm{1}+\mathrm{3}^{\mathrm{25}} \right)}{\mathrm{3}^{\mathrm{13}×\mathrm{25}} }=\mathrm{1} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}^{\mathrm{13}} }{\sqrt[{\mathrm{25}}]{\left(\mathrm{1}+\mathrm{3}\right)\left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} \right)...\left(\mathrm{1}+\mathrm{3}^{\mathrm{25}} \right)}} \\ $$
