
Question Number 101247 by 175 last updated on 01/Jul/20
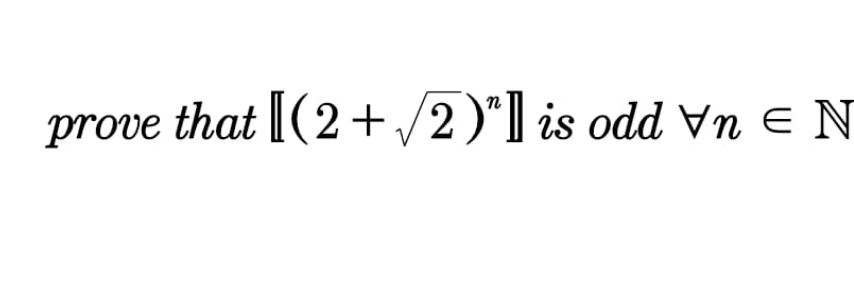
Answered by 1549442205 last updated on 06/Jul/20
![Note :the integral part of a real number x be the grearest integer which don′t exceed x and is denoted by symbol [x] Put A_n = (2+(√2))^n +(2−(√2))^n .Then we prove that A_n is even ∀n∈N .Indeed, i)For n=0 ⇒ A_0 =2.For n=1⇒A_1 =4 A_n =[(2+(√2))^n +(2−(√2))^n ]= [(2+(√2))^(n−1) +(2−(√2))^(n−1) ][(2+(√2))+(2−(√2))] −(2−(√2))(2+(√2))^(n−1) −(2+(√2))(2−(√2))^(n−1) =4.A_(n−1) −2(2+(√2))^(n−2) −2(2−(√2))^(n−2) =4.A_(n−1) −2A_(n−2) which shows that A_n is an even number ∀n∈N Now we see that 0<m=(2−(√2))^n <1 due to 2−(√2)<1.It follows that (2+(√2))^n =A_n −(2−(√2))^n =2M−m ⇒[(2+(√2))^n ]=2M−1 which means that [2+(√2))^n ]is odd(q.e.d)](Q101358.png)
$$\boldsymbol{\mathrm{Note}}\::\mathrm{the}\:\mathrm{integral}\:\mathrm{part}\:\mathrm{of}\:\mathrm{a}\:\mathrm{real}\:\mathrm{number} \\ $$$$\mathrm{x}\:\mathrm{be}\:\mathrm{the}\:\mathrm{grearest}\:\mathrm{integer}\:\mathrm{which}\:\mathrm{don}'\mathrm{t}\:\mathrm{exceed}\:\mathrm{x} \\ $$$$\mathrm{and}\:\mathrm{is}\:\mathrm{denoted}\:\mathrm{by}\:\mathrm{symbol}\:\left[\mathrm{x}\right] \\ $$$$\mathrm{Put}\:\mathrm{A}_{\mathrm{n}} =\:\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{n}} +\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{n}} .\mathrm{Then}\:\mathrm{we}\: \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{A}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{even}\:\forall\mathrm{n}\in\mathbb{N}\:.\mathrm{Indeed}, \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{n}=\mathrm{0}\:\Rightarrow\:\mathrm{A}_{\mathrm{0}} =\mathrm{2}.\mathrm{For}\:\mathrm{n}=\mathrm{1}\Rightarrow\mathrm{A}_{\mathrm{1}} =\mathrm{4} \\ $$$$\mathrm{A}_{\mathrm{n}} =\left[\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{n}} +\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \right]= \\ $$$$\left[\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{n}−\mathrm{1}} +\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{n}−\mathrm{1}} \right]\left[\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\right] \\ $$$$−\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{n}−\mathrm{1}} −\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{n}−\mathrm{1}} \\ $$$$=\mathrm{4}.\mathrm{A}_{\mathrm{n}−\mathrm{1}} −\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{n}−\mathrm{2}} −\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{n}−\mathrm{2}} \\ $$$$=\mathrm{4}.\mathrm{A}_{\mathrm{n}−\mathrm{1}} −\mathrm{2A}_{\mathrm{n}−\mathrm{2}} \mathrm{which}\:\mathrm{shows}\:\mathrm{that} \\ $$$$\mathrm{A}_{\mathrm{n}} \mathrm{is}\:\mathrm{an}\:\mathrm{even}\:\mathrm{number}\:\forall\mathrm{n}\in\mathbb{N} \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{see}\:\mathrm{that}\:\mathrm{0}<\mathrm{m}=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{n}} <\mathrm{1}\: \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{2}−\sqrt{\mathrm{2}}<\mathrm{1}.\mathrm{It}\:\mathrm{follows}\:\mathrm{that}\: \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{n}} =\mathrm{A}_{\mathrm{n}} −\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{n}} =\mathrm{2M}−\mathrm{m} \\ $$$$\Rightarrow\left[\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{\mathrm{n}}} \right]=\mathrm{2}\boldsymbol{\mathrm{M}}−\mathrm{1} \\ $$$$\left.\boldsymbol{\mathrm{which}}\:\boldsymbol{\mathrm{means}}\:\boldsymbol{\mathrm{that}}\:\left[\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{\mathrm{n}}} \right]\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{odd}}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$
