Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 100720 by bemath last updated on 28/Jun/20

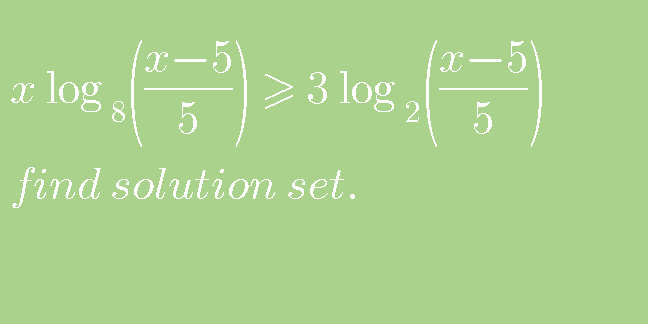
Commented by 1549442205 last updated on 28/Jun/20

one other way:the conditions for the inequality is defined as:((x−5)/5)>0⇔x>5 Since log_8 ((x−5)/5)=log_2 (((x−5)/5))^(1/3) ,so we get x.(1/3)log_2 ((x−5)/5)≥3log_2 ((x−5)/5) ⇔((x−9)/3).log_2 ((x−5)/5)≥0⇔]_( { ((x−9≤0)),((log_2 ((x−5)/5)≤0)) :} ⇔ { ((5<x≤9)),((x≤10)) :}⇔5<x≤9) ^( { ((x−9≥0)),((log_2 ((x−5)/5)≥0)) :} ⇔ { ((x≥9)),((x≥10)) :}⇔x≥10) Combining both cases we get solution set of the given inequality is (5;9]∪[10;+∞)

$$ \\ $$$$\mathrm{one}\:\mathrm{other}\:\mathrm{way}:\mathrm{the}\:\mathrm{conditions}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{inequality}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{as}:\frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}>\mathrm{0}\Leftrightarrow\mathrm{x}>\mathrm{5} \\ $$$$\mathrm{Since}\:\mathrm{log}_{\mathrm{8}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}=\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ,\mathrm{so}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}.\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}_{\mathrm{2}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}\geqslant\mathrm{3log}_{\mathrm{2}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}} \\ $$$$\left.\Leftrightarrow\frac{\mathrm{x}−\mathrm{9}}{\mathrm{3}}.\mathrm{log}_{\mathrm{2}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}\geqslant\mathrm{0}\Leftrightarrow\right]_{\begin{cases}{\mathrm{x}−\mathrm{9}\leqslant\mathrm{0}}\\{\mathrm{log}_{\mathrm{2}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}\leqslant\mathrm{0}}\end{cases}\:\:\Leftrightarrow\begin{cases}{\mathrm{5}<\mathrm{x}\leqslant\mathrm{9}}\\{\mathrm{x}\leqslant\mathrm{10}}\end{cases}\Leftrightarrow\mathrm{5}<\mathrm{x}\leqslant\mathrm{9}} ^{\begin{cases}{\mathrm{x}−\mathrm{9}\geqslant\mathrm{0}}\\{\mathrm{log}_{\mathrm{2}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}\geqslant\mathrm{0}}\end{cases}\:\:\:\:\Leftrightarrow\begin{cases}{\mathrm{x}\geqslant\mathrm{9}}\\{\mathrm{x}\geqslant\mathrm{10}}\end{cases}\Leftrightarrow\mathrm{x}\geqslant\mathrm{10}} \\ $$$$\mathrm{Combining}\:\mathrm{both}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:\mathrm{set} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{is}\:\left(\mathrm{5};\mathrm{9}\right]\cup\left[\mathrm{10};+\infty\right) \\ $$

Commented by Rasheed.Sindhi last updated on 28/Jun/20

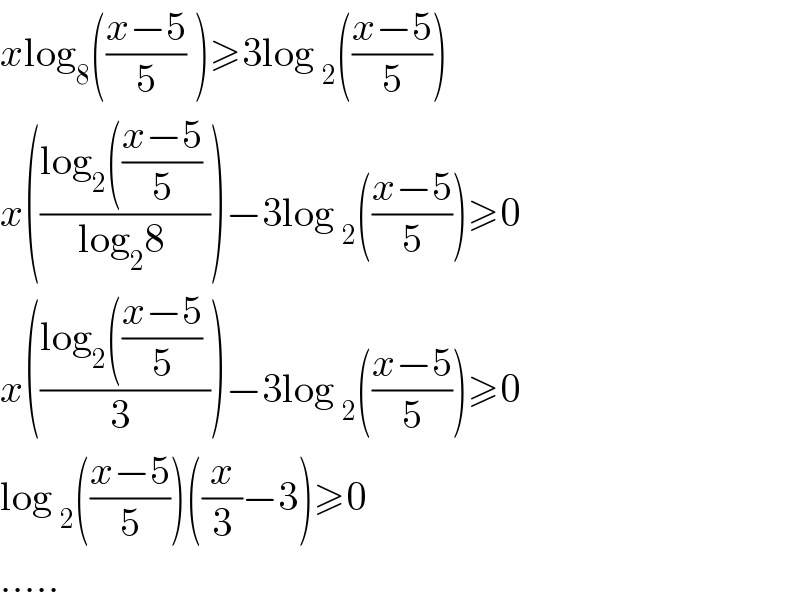
xlog_8 (((x−5)/5) )≥3log _2 (((x−5)/5)) x(((log_2 (((x−5)/5) )/(log_2 8 )))−3log _2 (((x−5)/5))≥0 x(((log_2 (((x−5)/5) )/(3 )))−3log _2 (((x−5)/5))≥0 log _2 (((x−5)/5))((x/3)−3)≥0 .....

$${x}\mathrm{log}_{\mathrm{8}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\:\right)\geqslant\mathrm{3log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right) \\ $$$${x}\left(\frac{\mathrm{log}_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\:\right.}{\mathrm{log}_{\mathrm{2}} \mathrm{8}\:}\right)−\mathrm{3log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\geqslant\mathrm{0} \\ $$$${x}\left(\frac{\mathrm{log}_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\:\right.}{\mathrm{3}\:}\right)−\mathrm{3log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\left(\frac{{x}}{\mathrm{3}}−\mathrm{3}\right)\geqslant\mathrm{0} \\ $$$$..... \\ $$

Commented by bramlex last updated on 28/Jun/20

⇔(1/3)x log _2 (((x−5)/5))−3log _2 (((x−5)/5)) ≥ 0 ((1/3)x−3)(log _2 (((x−5)/5))) ≥ 0 (((x−9)/3))(log _2 (((x−5)/5))) ≥ 0 case(1) x ≥ 9 ∧ log _2 (((x−5)/5))≥0 x ≥ 10 ⇒ x ≥ 10 case(2) x ≤9 ∧ log _2 (((x−5)/5))≤0 x ≤10 ⇒x ≤9 inequality defined on x>5 hence the solution set is {x/ 5<x≤9 ∪ x ≥10 }

$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{3}}{x}\:\mathrm{log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)−\mathrm{3log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\:\geqslant\:\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{3}}{x}−\mathrm{3}\right)\left(\mathrm{log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\right)\:\geqslant\:\mathrm{0} \\ $$$$\left(\frac{{x}−\mathrm{9}}{\mathrm{3}}\right)\left(\mathrm{log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\right)\:\geqslant\:\mathrm{0} \\ $$$${case}\left(\mathrm{1}\right)\:{x}\:\geqslant\:\mathrm{9}\:\wedge\:\mathrm{log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\geqslant\mathrm{0} \\ $$$${x}\:\geqslant\:\mathrm{10}\:\Rightarrow\:{x}\:\geqslant\:\mathrm{10} \\ $$$${case}\left(\mathrm{2}\right)\:{x}\:\leqslant\mathrm{9}\:\wedge\:\mathrm{log}\:_{\mathrm{2}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\leqslant\mathrm{0} \\ $$$${x}\:\leqslant\mathrm{10}\:\Rightarrow{x}\:\leqslant\mathrm{9} \\ $$$${inequality}\:{defined}\:{on}\:{x}>\mathrm{5}\: \\ $$$${hence}\:{the}\:{solution}\:{set}\:{is} \\ $$$$\left\{{x}/\:\mathrm{5}<{x}\leqslant\mathrm{9}\:\cup\:{x}\:\geqslant\mathrm{10}\:\right\} \\ $$

Answered by mahdi last updated on 28/Jun/20

log_8 ((x−5)/5)=(1/3)log_2 ((x−5)/5)=u t>0 x.u≥9u I { ((if u>0⇒x≥9)),((log_8 ((x−5)/5)>0 ⇒((x−5)/5)>1⇒x>10)) :}⇒x>10 II { ((if u<0⇒x≤9)),((log_8 ((x−5)/5)<0 ⇒0<((x−5)/5)<1⇒5<x<10)) :}⇒5<x≤9 III { ((if u=0⇒∀x,x×0≥9×0)),((log_8 ((x−5)/5)=0 ⇒((x−5)/5)=1⇒x=10)) :}⇒x=10 I∪II∪III=x∈(5,9]∪[10,+∞)

$$\mathrm{log}_{\mathrm{8}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}_{\mathrm{2}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}=\mathrm{u}\:\:\:\:\mathrm{t}>\mathrm{0} \\ $$$$\mathrm{x}.\mathrm{u}\geqslant\mathrm{9u} \\ $$$$\mathrm{I\begin{cases}{\mathrm{if}\:\:\:\mathrm{u}>\mathrm{0}\Rightarrow\mathrm{x}\geqslant\mathrm{9}}\\{\mathrm{log}_{\mathrm{8}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}>\mathrm{0}\:\Rightarrow\frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}>\mathrm{1}\Rightarrow\mathrm{x}>\mathrm{10}}\end{cases}}\Rightarrow\mathrm{x}>\mathrm{10} \\ $$$$\mathrm{II\begin{cases}{\mathrm{if}\:\:\:\mathrm{u}<\mathrm{0}\Rightarrow\mathrm{x}\leqslant\mathrm{9}}\\{\mathrm{log}_{\mathrm{8}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}<\mathrm{0}\:\Rightarrow\mathrm{0}<\frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}<\mathrm{1}\Rightarrow\mathrm{5}<\mathrm{x}<\mathrm{10}}\end{cases}}\Rightarrow\mathrm{5}<\mathrm{x}\leqslant\mathrm{9} \\ $$$$\mathrm{III\begin{cases}{\mathrm{if}\:\:\:\mathrm{u}=\mathrm{0}\Rightarrow\forall\mathrm{x},\mathrm{x}×\mathrm{0}\geqslant\mathrm{9}×\mathrm{0}}\\{\mathrm{log}_{\mathrm{8}} \frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}=\mathrm{0}\:\Rightarrow\frac{\mathrm{x}−\mathrm{5}}{\mathrm{5}}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{10}}\end{cases}}\Rightarrow\mathrm{x}=\mathrm{10} \\ $$$$\mathrm{I}\cup\mathrm{II}\cup\mathrm{III}=\mathrm{x}\in\left(\mathrm{5},\mathrm{9}\right]\cup\left[\mathrm{10},+\infty\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com