
Question Number 73668 by liki last updated on 14/Nov/19
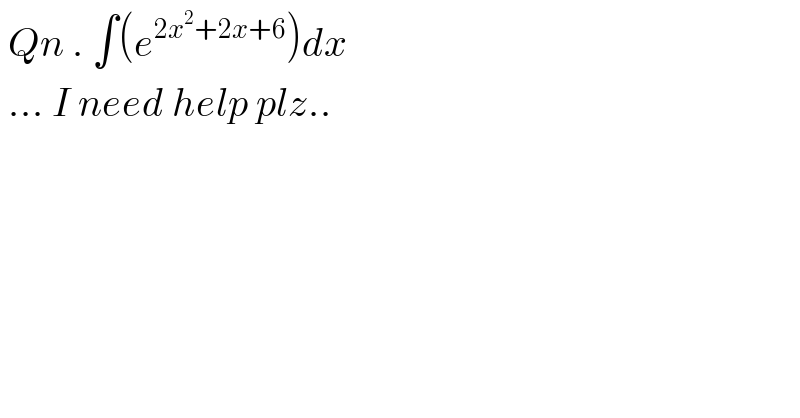
$$\:{Qn}\:.\:\int\left({e}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{6}} \right){dx} \\ $$$$\:...\:{I}\:{need}\:{help}\:{plz}.. \\ $$$$ \\ $$$$ \\ $$
Answered by arkanmath7@gmail.com last updated on 14/Nov/19

$$=\:\int{e}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}\:} .\:{e}^{\mathrm{6}} \:{dx} \\ $$$$=\:{e}^{\mathrm{6}} \int{e}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}\:} {dx} \\ $$$$=\:{e}^{\mathrm{6}} \int{e}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:} {dx}\: \\ $$$$=\:{e}^{\mathrm{6}} \int{e}^{\left(\sqrt{\mathrm{2}}{x}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\:} {dx}\: \\ $$$$={e}^{−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{\mathrm{6}} \int{e}^{\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:} {dx}\: \\ $$$$ \\ $$$${now}\:{let}\:{u}\:=\:\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{2}}}\:\:\Rightarrow\:{du}\:=\:\sqrt{\mathrm{2}\:}{dx} \\ $$$$\:\:\Rightarrow\:{du}\:=\:\sqrt{\mathrm{2}\:}{dx}\:\Rightarrow\:{dx}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:{du} \\ $$$$\int{e}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{6}} {dx}\:=\:{e}^{\frac{\mathrm{11}}{\mathrm{2}}} \:.\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\int{e}^{{u}^{\mathrm{2}} } {du} \\ $$$$\:=\:\:\frac{\sqrt{\pi}{e}^{\frac{\mathrm{11}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\mathrm{2}}}\:\int\frac{\mathrm{2}{e}^{{u}^{\mathrm{2}} } }{\sqrt{\pi}}{du}\:\:\:\:\:{error}\:{function} \\ $$$$\:=\:\:\frac{\sqrt{\pi}{e}^{\frac{\mathrm{11}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\mathrm{2}}}\:{erf}\left({u}\right) \\ $$$$\:=\:\:\frac{\sqrt{\pi}{e}^{\frac{\mathrm{11}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\mathrm{2}}}\:{erf}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{2}}}\right)\:+\:{c} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by liki last updated on 14/Nov/19
$$\:\:{Thanks}\:{so}\:{much}.. \\ $$
Commented by liki last updated on 14/Nov/19
well soln
