
Question Number 188881 by mnjuly1970 last updated on 08/Mar/23
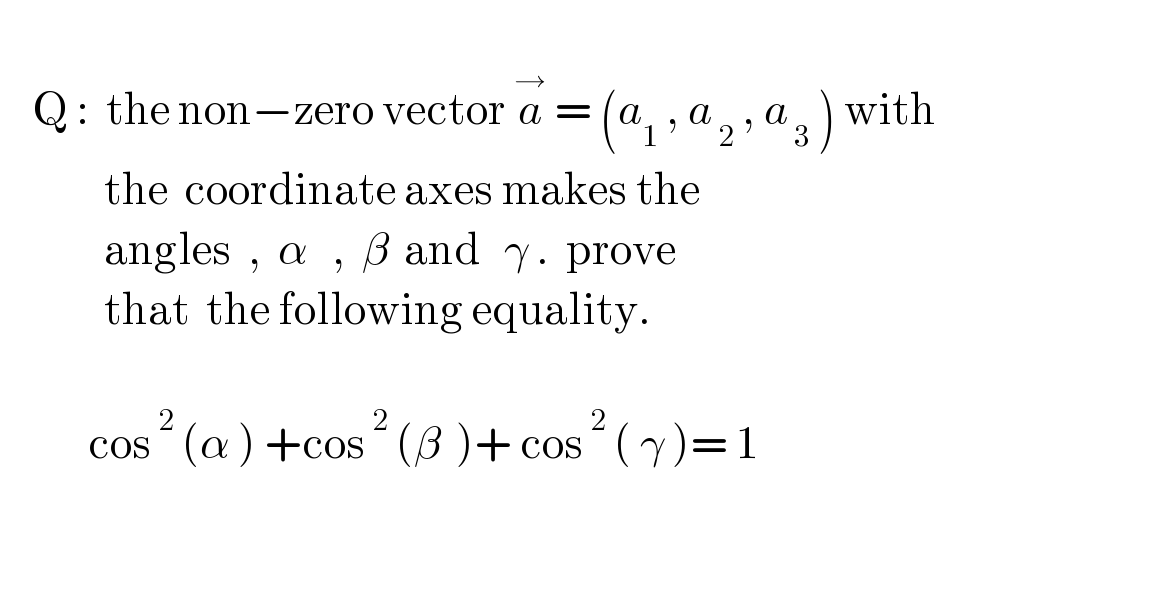
$$ \\ $$$$\:\:\:\:\mathrm{Q}\::\:\:\mathrm{the}\:\mathrm{non}−\mathrm{zero}\:\mathrm{vector}\:\overset{\rightarrow} {{a}}\:=\:\left({a}_{\mathrm{1}} \:,\:{a}_{\:\mathrm{2}} \:,\:{a}_{\:\mathrm{3}} \:\right)\:\mathrm{with} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{the}\:\:\mathrm{coordinate}\:\mathrm{axes}\:\mathrm{makes}\:\mathrm{the} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{angles}\:\:,\:\:\alpha\:\:\:,\:\:\beta\:\:\mathrm{and}\:\:\:\gamma\:.\:\:\mathrm{prove} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{that}\:\:\mathrm{the}\:\mathrm{following}\:\mathrm{equality}. \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}^{\:\mathrm{2}} \:\left(\alpha\:\right)\:+\mathrm{cos}^{\:\mathrm{2}} \:\left(\beta\:\:\right)+\:\mathrm{cos}^{\:\mathrm{2}} \:\left(\:\gamma\:\right)=\:\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 08/Mar/23
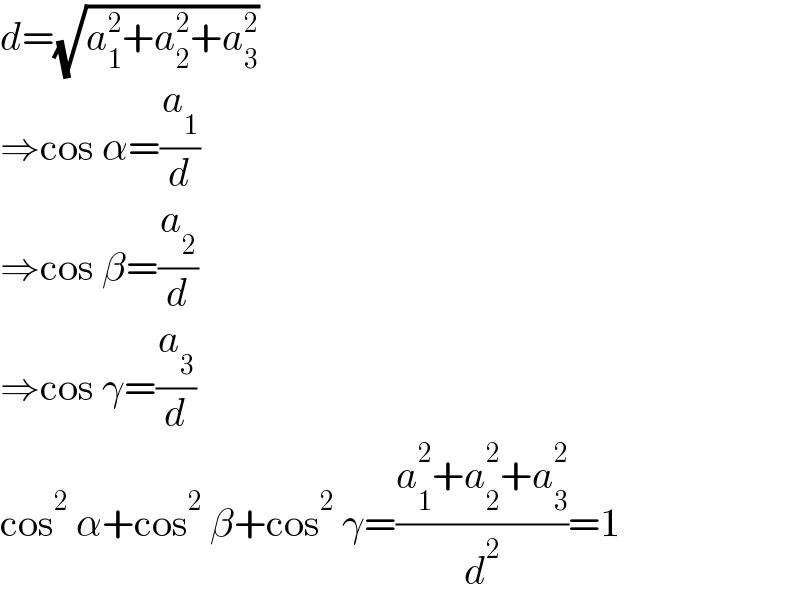
$${d}=\sqrt{{a}_{\mathrm{1}} ^{\mathrm{2}} +{a}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{3}} ^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{{a}_{\mathrm{1}} }{{d}} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{{a}_{\mathrm{2}} }{{d}} \\ $$$$\Rightarrow\mathrm{cos}\:\gamma=\frac{{a}_{\mathrm{3}} }{{d}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\alpha+\mathrm{cos}^{\mathrm{2}} \:\beta+\mathrm{cos}^{\mathrm{2}} \:\gamma=\frac{{a}_{\mathrm{1}} ^{\mathrm{2}} +{a}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{3}} ^{\mathrm{2}} }{{d}^{\mathrm{2}} }=\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 08/Mar/23

$${thanks}\:{alot}\:{sir}\:{W} \\ $$
