Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 201263 by mnjuly1970 last updated on 02/Dec/23

Q: the equation , sin^( 2) (x)−sin(mx)cos^2 (x)=1 has four distinct roots in ( 0 , 2π ) find the values of , m . (m ∈ N )

$$ \\ $$$$\:\:\:\:{Q}:\:{the}\:{equation}\:,\:{sin}^{\:\mathrm{2}} \left({x}\right)−{sin}\left({mx}\right){cos}\:^{\mathrm{2}} \left({x}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{has}\:\:{four}\:{distinct}\:{roots} \\ $$$$\:\:\:\:\:\:\:{in}\:\left(\:\mathrm{0}\:,\:\mathrm{2}\pi\:\right)\:\:{find}\:{the}\:{values} \\ $$$$\:\:\:\:\:\:\:\:{of}\:\:,\:\:\:{m}\:\:\:.\:\:\left({m}\:\in\:\mathbb{N}\:\right) \\ $$$$ \\ $$

Answered by MM42 last updated on 03/Dec/23

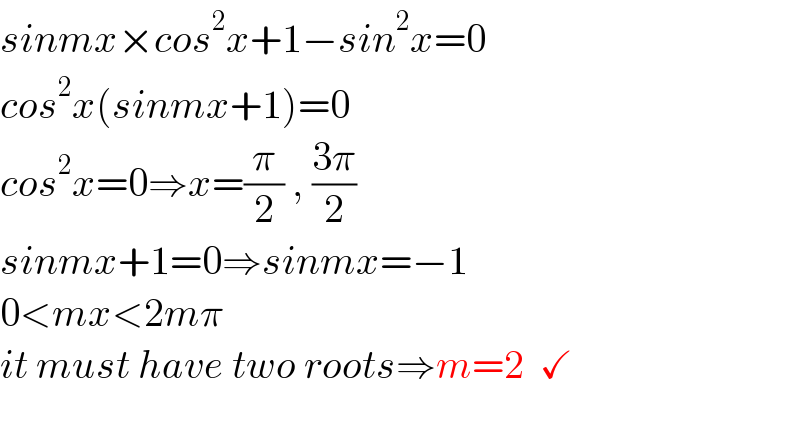
sinmx×cos^2 x+1−sin^2 x=0 cos^2 x(sinmx+1)=0 cos^2 x=0⇒x=(π/2) , ((3π)/2) sinmx+1=0⇒sinmx=−1 0<mx<2mπ it must have two roots⇒m=2 ✓

$${sinmx}×{cos}^{\mathrm{2}} {x}+\mathrm{1}−{sin}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$${cos}^{\mathrm{2}} {x}\left({sinmx}+\mathrm{1}\right)=\mathrm{0} \\ $$$${cos}^{\mathrm{2}} {x}=\mathrm{0}\Rightarrow{x}=\frac{\pi}{\mathrm{2}}\:,\:\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${sinmx}+\mathrm{1}=\mathrm{0}\Rightarrow{sinmx}=−\mathrm{1} \\ $$$$\mathrm{0}<{mx}<\mathrm{2}{m}\pi \\ $$$${it}\:{must}\:{have}\:{two}\:{roots}\Rightarrow{m}=\mathrm{2}\:\:\checkmark \\ $$$$ \\ $$

Answered by mr W last updated on 03/Dec/23

sin^2 x−sin mx cos^2 x=1 cos^2 x (sin mx+1)=0 ⇒cos x=0 ⇒x=(π/2), ((3π)/2) ⇒sin mx+1=0 ⇒sin mx=−1 ⇒mx=2kπ−(π/2) ⇒x=(1/m)(2kπ−(π/2)) there must be two values for x∈(0, 2π) which are different than (π/2) and ((3π)/2). 0<(1/m)(2kπ−(π/2))<2π 0<((4k−1)/m)<4 (1/m)(2kπ−(π/2))≠(π/2) ⇒k≠((m+1)/4) (1/m)(2kπ−(π/2))≠((3π)/2) ⇒k≠((3m+1)/4) case m>0: 0<4k−1<4m (1/4)<k<m+(1/4) ⇒1≤k≤m two pairs (k, m): m=2 and k=1, 2. or three pairs (k, m): m=3 and k=1, 2, 3 (with k=1 for x=(π/2)). case m<0: 4m<4k−1<0 m+(1/4)<k<(1/4) ⇒m+1≤k≤0 two pairs (k, m) m=−2 and k=−1, 0. or three pairs (k, m): m=−3 and k=−2, −1, 0 (with k=−2 for x=(π/2)) summary: for m∈Z: m=±2, ±3 for m∈N: m=2, 3

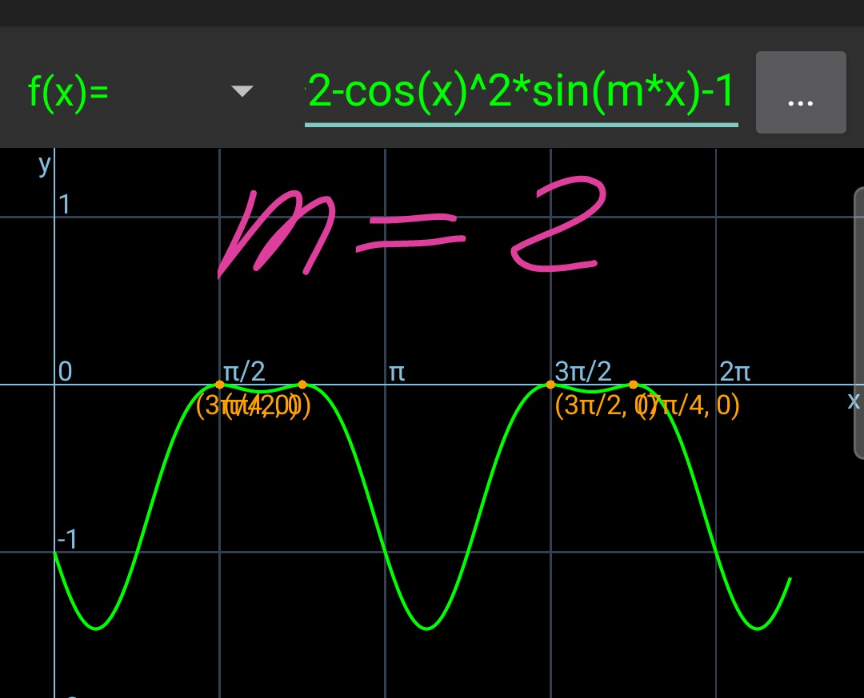
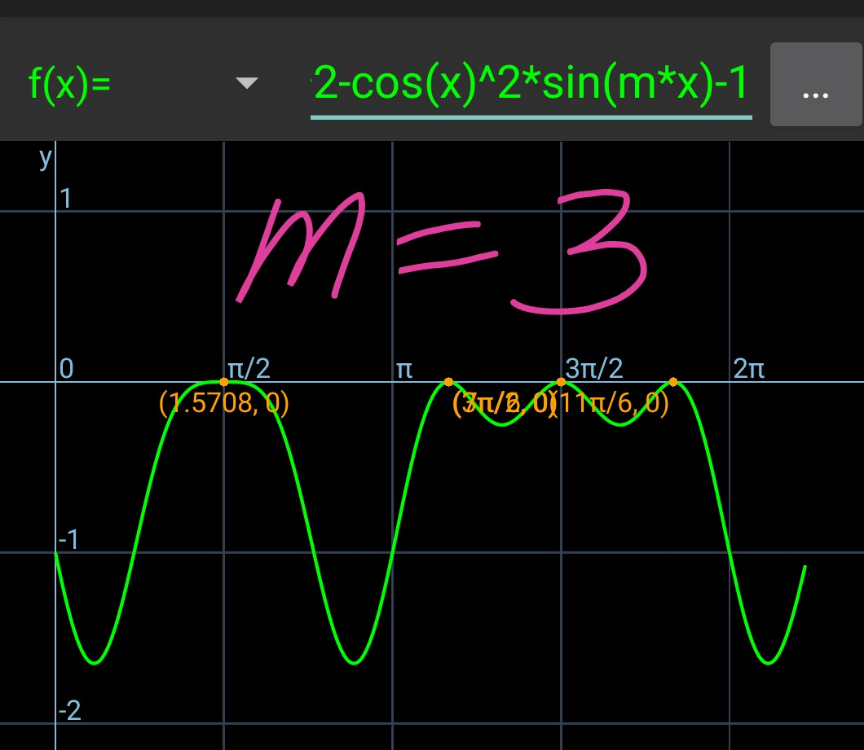
$$\mathrm{sin}^{\mathrm{2}} \:{x}−\mathrm{sin}\:{mx}\:\mathrm{cos}^{\mathrm{2}} \:{x}=\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:\left(\mathrm{sin}\:{mx}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:{x}=\mathrm{0}\:\Rightarrow{x}=\frac{\pi}{\mathrm{2}},\:\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:{mx}+\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{sin}\:{mx}=−\mathrm{1}\:\Rightarrow{mx}=\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{{m}}\left(\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}}\right) \\ $$$${there}\:{must}\:{be}\:{two}\:{values}\:{for}\:{x}\in\left(\mathrm{0},\:\mathrm{2}\pi\right) \\ $$$${which}\:{are}\:{different}\:{than}\:\frac{\pi}{\mathrm{2}}\:{and}\:\frac{\mathrm{3}\pi}{\mathrm{2}}. \\ $$$$\mathrm{0}<\frac{\mathrm{1}}{{m}}\left(\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}}\right)<\mathrm{2}\pi \\ $$$$\mathrm{0}<\frac{\mathrm{4}{k}−\mathrm{1}}{{m}}<\mathrm{4} \\ $$$$\frac{\mathrm{1}}{{m}}\left(\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}}\right)\neq\frac{\pi}{\mathrm{2}}\:\Rightarrow{k}\neq\frac{{m}+\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{{m}}\left(\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}}\right)\neq\frac{\mathrm{3}\pi}{\mathrm{2}}\:\Rightarrow{k}\neq\frac{\mathrm{3}{m}+\mathrm{1}}{\mathrm{4}} \\ $$$${case}\:{m}>\mathrm{0}:\:\: \\ $$$$\mathrm{0}<\mathrm{4}{k}−\mathrm{1}<\mathrm{4}{m} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}<{k}<{m}+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{1}\leqslant{k}\leqslant{m} \\ $$$${two}\:{pairs}\:\left({k},\:{m}\right): \\ $$$${m}=\mathrm{2}\:{and}\:{k}=\mathrm{1},\:\mathrm{2}. \\ $$$${or}\:{three}\:{pairs}\:\left({k},\:{m}\right): \\ $$$${m}=\mathrm{3}\:{and}\:{k}=\mathrm{1},\:\mathrm{2},\:\mathrm{3}\:\left({with}\:{k}=\mathrm{1}\:{for}\:{x}=\frac{\pi}{\mathrm{2}}\right). \\ $$$${case}\:{m}<\mathrm{0}: \\ $$$$\mathrm{4}{m}<\mathrm{4}{k}−\mathrm{1}<\mathrm{0} \\ $$$${m}+\frac{\mathrm{1}}{\mathrm{4}}<{k}<\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{m}+\mathrm{1}\leqslant{k}\leqslant\mathrm{0} \\ $$$${two}\:{pairs}\:\left({k},\:{m}\right) \\ $$$${m}=−\mathrm{2}\:{and}\:{k}=−\mathrm{1},\:\mathrm{0}. \\ $$$${or}\:{three}\:{pairs}\:\left({k},\:{m}\right): \\ $$$${m}=−\mathrm{3}\:{and}\:{k}=−\mathrm{2},\:−\mathrm{1},\:\mathrm{0}\:\left({with}\:{k}=−\mathrm{2}\:{for}\:{x}=\frac{\pi}{\mathrm{2}}\right) \\ $$$$\boldsymbol{{summary}}: \\ $$$${for}\:{m}\in{Z}:\:{m}=\pm\mathrm{2},\:\pm\mathrm{3} \\ $$$${for}\:{m}\in{N}:\:{m}=\mathrm{2},\:\mathrm{3} \\ $$

Commented by mr W last updated on 03/Dec/23

Commented by mr W last updated on 03/Dec/23

Commented by mnjuly1970 last updated on 03/Dec/23

thanks alot sir

$${thanks}\:{alot}\:{sir} \\ $$

Commented by mnjuly1970 last updated on 03/Dec/23

excelent sir

$${excelent}\:{sir} \\ $$

Commented by MM42 last updated on 03/Dec/23

⋛

$$ \\ $$$$\:\cancel{\lesseqgtr} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com