
Question Number 191512 by mnjuly1970 last updated on 25/Apr/23
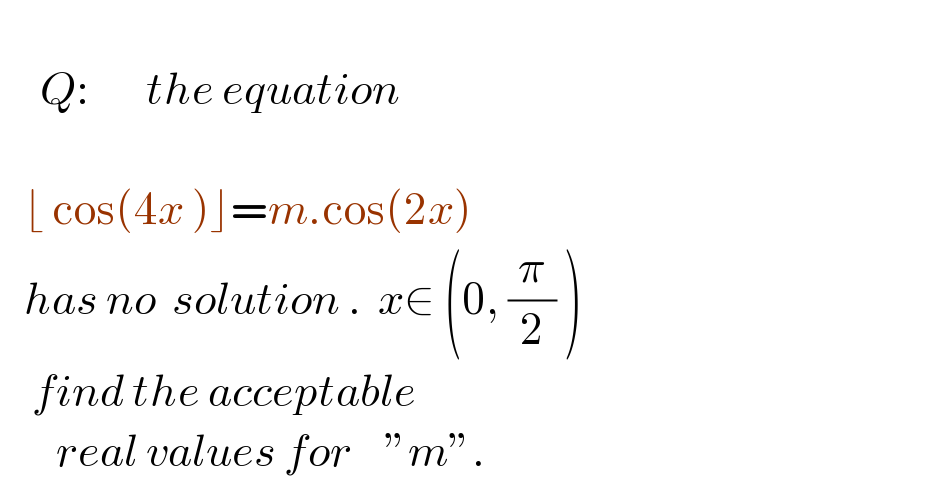
$$ \\ $$$$\:\:\:\:\:{Q}:\:\:\:\:\:\:\:{the}\:{equation}\: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\lfloor\:\mathrm{cos}\left(\mathrm{4}{x}\:\right)\rfloor={m}.\mathrm{cos}\left(\mathrm{2}{x}\right) \\ $$$$\:\:\:{has}\:{no}\:\:{solution}\:.\:\:{x}\in\:\left(\mathrm{0},\:\frac{\pi}{\mathrm{2}}\:\right) \\ $$$$\:\:\:\:{find}\:{the}\:{acceptable} \\ $$$$\:\:\:\:\:\:\:{real}\:{values}\:{for}\:\:\:\:''{m}''. \\ $$
Answered by mahdipoor last updated on 26/Apr/23
![[cos(4x)]=0,1,−1 ⇒^(no answer) mcos(2x)≠0,1,−1 m≠((0,1,−1)/(cos(2x))) ⇒^(1<cosx<−1) m≠0,R−(−1,−1) ⇒⇒m=[−1,1]](Q191585.png)
$$\left[{cos}\left(\mathrm{4}{x}\right)\right]=\mathrm{0},\mathrm{1},−\mathrm{1}\:\:\overset{{no}\:{answer}} {\Rightarrow}\:\:\:{mcos}\left(\mathrm{2}{x}\right)\neq\mathrm{0},\mathrm{1},−\mathrm{1} \\ $$$${m}\neq\frac{\mathrm{0},\mathrm{1},−\mathrm{1}}{{cos}\left(\mathrm{2}{x}\right)}\:\:\:\overset{\mathrm{1}<{cosx}<−\mathrm{1}} {\Rightarrow}\:\:\:{m}\neq\mathrm{0},{R}−\left(−\mathrm{1},−\mathrm{1}\right) \\ $$$$\Rightarrow\Rightarrow{m}=\left[−\mathrm{1},\mathrm{1}\right] \\ $$
