
Question Number 78358 by aliesam last updated on 16/Jan/20
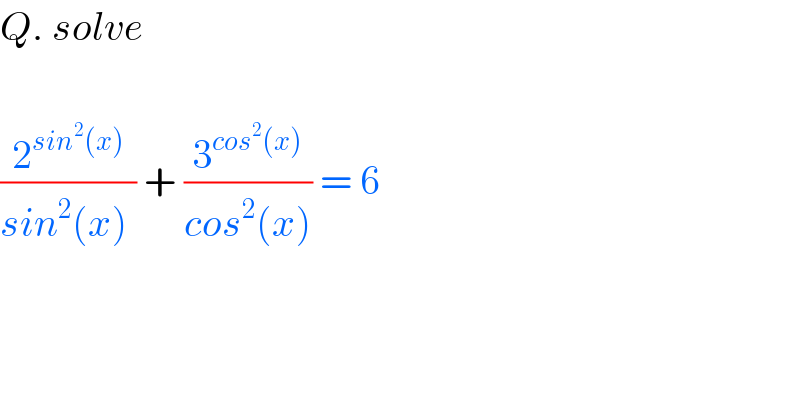
$${Q}.\:{solve} \\ $$$$ \\ $$$$\frac{\mathrm{2}^{{sin}^{\mathrm{2}} \left({x}\right)} }{{sin}^{\mathrm{2}} \left({x}\right)\:}\:+\:\frac{\mathrm{3}^{{cos}^{\mathrm{2}} \left({x}\right)} }{{cos}^{\mathrm{2}} \left({x}\right)}\:=\:\mathrm{6} \\ $$
Commented by MJS last updated on 16/Jan/20

$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lhs}\:\mathrm{is}\:\mathrm{2}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)>\mathrm{6}\:\mathrm{at} \\ $$$${x}=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}{n}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\in\mathbb{R} \\ $$
