Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199109 by mnjuly1970 last updated on 28/Oct/23

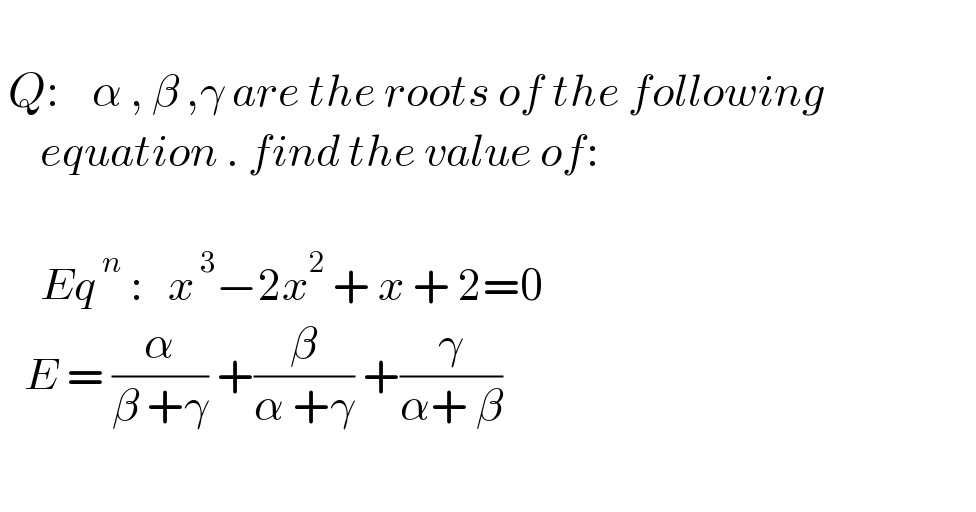
Q: α , β ,γ are the roots of the following equation . find the value of: Eq^( n) : x^( 3) −2x^2 + x + 2=0 E = (α/(β +γ)) +(β/(α +γ)) +(γ/(α+ β))

$$ \\ $$$$\:{Q}:\:\:\:\:\alpha\:,\:\beta\:,\gamma\:{are}\:{the}\:{roots}\:{of}\:{the}\:{following} \\ $$$$\:\:\:\:\:{equation}\:.\:{find}\:{the}\:{value}\:{of}: \\ $$$$ \\ $$$$\:\:\:\:\:{Eq}^{\:{n}} \::\:\:\:{x}^{\:\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:{E}\:=\:\frac{\alpha}{\beta\:+\gamma}\:+\frac{\beta}{\alpha\:+\gamma}\:+\frac{\gamma}{\alpha+\:\beta} \\ $$$$ \\ $$

Commented by cortano12 last updated on 28/Oct/23

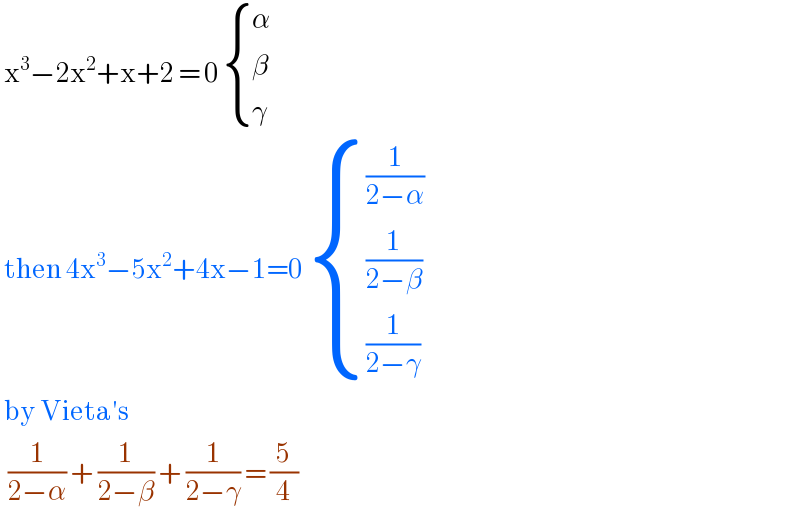
x^3 −2x^2 +x+2 = 0 { (α),(β),(γ) :} then 4x^3 −5x^2 +4x−1=0 { ((1/(2−α))),((1/(2−β))),((1/(2−γ))) :} by Vieta′s (1/(2−α)) + (1/(2−β)) + (1/(2−γ)) = (5/4)

$$\:\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}\:=\:\mathrm{0}\:\begin{cases}{\alpha}\\{\beta}\\{\gamma}\end{cases}\: \\ $$$$\:\mathrm{then}\:\mathrm{4x}^{\mathrm{3}} −\mathrm{5x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{1}=\mathrm{0}\:\begin{cases}{\frac{\mathrm{1}}{\mathrm{2}−\alpha}}\\{\frac{\mathrm{1}}{\mathrm{2}−\beta}}\\{\frac{\mathrm{1}}{\mathrm{2}−\gamma}}\end{cases}\:\:\:\:\:\: \\ $$$$\:\mathrm{by}\:\mathrm{Vieta}'\mathrm{s}\: \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{2}−\alpha}\:+\:\frac{\mathrm{1}}{\mathrm{2}−\beta}\:+\:\frac{\mathrm{1}}{\mathrm{2}−\gamma}\:=\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$

Answered by cortano12 last updated on 28/Oct/23

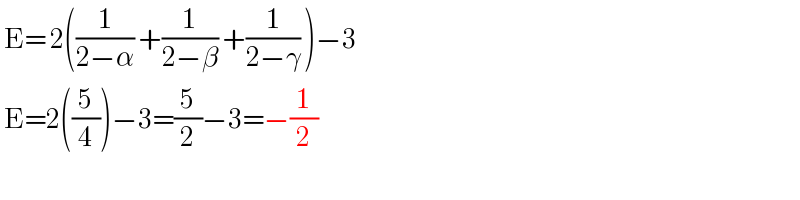
E= 2((1/(2−α)) +(1/(2−β)) +(1/(2−γ)) )−3 E=2((5/4))−3=(5/2)−3=−(1/2)

$$\:\mathrm{E}=\:\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}−\alpha}\:+\frac{\mathrm{1}}{\mathrm{2}−\beta}\:+\frac{\mathrm{1}}{\mathrm{2}−\gamma}\:\right)−\mathrm{3} \\ $$$$\:\mathrm{E}=\mathrm{2}\left(\frac{\mathrm{5}}{\mathrm{4}}\right)−\mathrm{3}=\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{3}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Oct/23

α,β,γ are roots of x^( 3) −2x^2 + x + 2=0 E = (α/(β +γ)) +(β/(α +γ)) +(γ/(α+ β))=? α+β+γ=−(−2)=2 αβ+βγ+γα=1 αβγ=−2 E+3= (α/(β +γ))+1 +(β/(α +γ))+1 +(γ/(α+ β))+1 = ((α+β +γ)/(β +γ)) +((β+α +γ)/(α +γ)) +((γ+α+ β)/(α+ β)) =(α+β +γ)((1/(β +γ)) +(1/(α +γ)) +(1/(α+ β))) =(α+β +γ)((1/(α+β +γ−α)) +(1/(α+β +γ−β)) +(1/(α+ β+γ−γ))) =(2)((1/(2−α)) +(1/(2−β)) +(1/(2−γ))) ((E+3)/2)=(((2−α)(2−β)+(2−β)(2−γ)+(2−γ)(2−α))/((2−α)(2−β)(2−γ))) =((−4(α+β+γ)+(αβ+βγ+γα)+12)/(8−αβγ−4(α+β+γ)+2(αβ+βγ+γα))) =((−4(2)+(1)+12)/(8−(−2)−4(2)+2(1)))=(5/4) E=(5/4)×2−3=−(1/2) ✓

$$\:\alpha,\beta,\gamma\:{are}\:{roots}\:{of}\:\:{x}^{\:\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{2}=\mathrm{0} \\ $$$${E}\:=\:\frac{\alpha}{\beta\:+\gamma}\:+\frac{\beta}{\alpha\:+\gamma}\:+\frac{\gamma}{\alpha+\:\beta}=? \\ $$$$\: \\ $$$$\alpha+\beta+\gamma=−\left(−\mathrm{2}\right)=\mathrm{2} \\ $$$$\alpha\beta+\beta\gamma+\gamma\alpha=\mathrm{1} \\ $$$$\alpha\beta\gamma=−\mathrm{2} \\ $$$${E}+\mathrm{3}=\:\frac{\alpha}{\beta\:+\gamma}+\mathrm{1}\:+\frac{\beta}{\alpha\:+\gamma}+\mathrm{1}\:+\frac{\gamma}{\alpha+\:\beta}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\alpha+\beta\:+\gamma}{\beta\:+\gamma}\:+\frac{\beta+\alpha\:+\gamma}{\alpha\:+\gamma}\:+\frac{\gamma+\alpha+\:\beta}{\alpha+\:\beta} \\ $$$$\:\:\:\:=\left(\alpha+\beta\:+\gamma\right)\left(\frac{\mathrm{1}}{\beta\:+\gamma}\:+\frac{\mathrm{1}}{\alpha\:+\gamma}\:+\frac{\mathrm{1}}{\alpha+\:\beta}\right) \\ $$$$\:=\left(\alpha+\beta\:+\gamma\right)\left(\frac{\mathrm{1}}{\alpha+\beta\:+\gamma−\alpha}\:+\frac{\mathrm{1}}{\alpha+\beta\:+\gamma−\beta}\:+\frac{\mathrm{1}}{\alpha+\:\beta+\gamma−\gamma}\right) \\ $$$$\:=\left(\mathrm{2}\right)\left(\frac{\mathrm{1}}{\mathrm{2}−\alpha}\:+\frac{\mathrm{1}}{\mathrm{2}−\beta}\:+\frac{\mathrm{1}}{\mathrm{2}−\gamma}\right) \\ $$$$\:\frac{{E}+\mathrm{3}}{\mathrm{2}}=\frac{\left(\mathrm{2}−\alpha\right)\left(\mathrm{2}−\beta\right)+\left(\mathrm{2}−\beta\right)\left(\mathrm{2}−\gamma\right)+\left(\mathrm{2}−\gamma\right)\left(\mathrm{2}−\alpha\right)}{\left(\mathrm{2}−\alpha\right)\left(\mathrm{2}−\beta\right)\left(\mathrm{2}−\gamma\right)} \\ $$$$\:\:\:\:\:\:\:=\frac{−\mathrm{4}\left(\alpha+\beta+\gamma\right)+\left(\alpha\beta+\beta\gamma+\gamma\alpha\right)+\mathrm{12}}{\mathrm{8}−\alpha\beta\gamma−\mathrm{4}\left(\alpha+\beta+\gamma\right)+\mathrm{2}\left(\alpha\beta+\beta\gamma+\gamma\alpha\right)} \\ $$$$\:\:\:\:\:\:\:=\frac{−\mathrm{4}\left(\mathrm{2}\right)+\left(\mathrm{1}\right)+\mathrm{12}}{\mathrm{8}−\left(−\mathrm{2}\right)−\mathrm{4}\left(\mathrm{2}\right)+\mathrm{2}\left(\mathrm{1}\right)}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${E}=\frac{\mathrm{5}}{\mathrm{4}}×\mathrm{2}−\mathrm{3}=−\frac{\mathrm{1}}{\mathrm{2}}\:\checkmark \\ $$

Commented by mnjuly1970 last updated on 30/Oct/23

thanks alot sir?

$${thanks}\:\:{alot}\:{sir}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com