
Question Number 191821 by mehdee42 last updated on 01/May/23
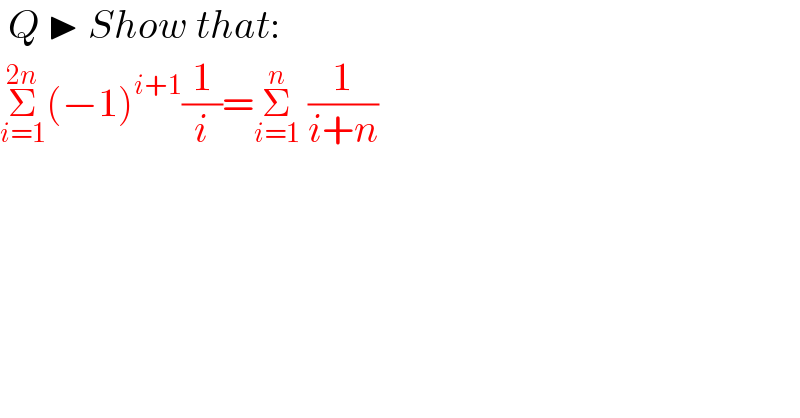
$$\:{Q}\:\blacktriangleright\:{Show}\:{that}: \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{i}+\mathrm{1}} \frac{\mathrm{1}}{{i}}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{i}+{n}} \\ $$
Answered by mehdee42 last updated on 03/May/23
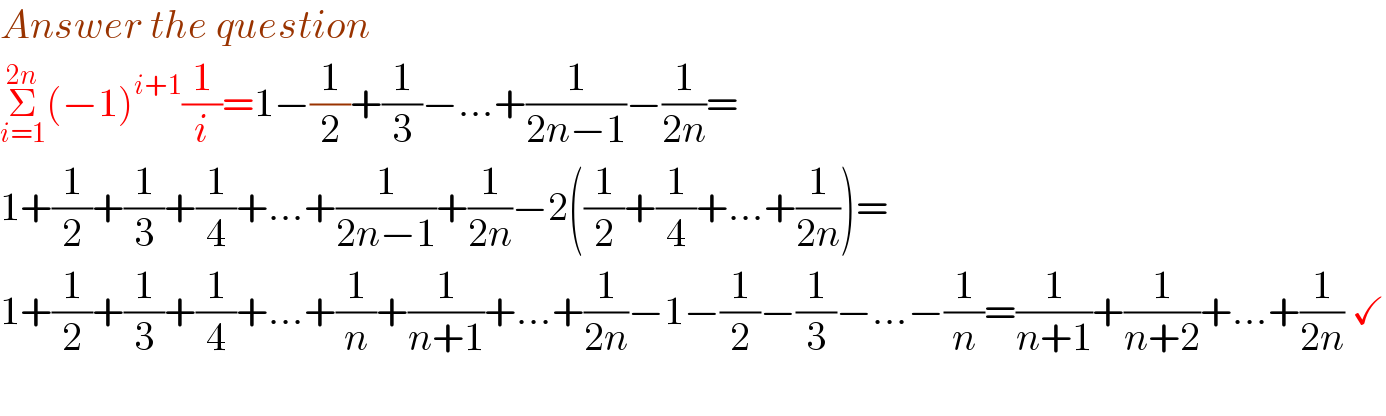
$${Answer}\:{the}\:{question} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{i}+\mathrm{1}} \frac{\mathrm{1}}{{i}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−...+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}}= \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)= \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}−...−\frac{\mathrm{1}}{{n}}=\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}\:\checkmark \\ $$$$ \\ $$
