
Question Number 35367 by Rio Mike last updated on 18/May/18
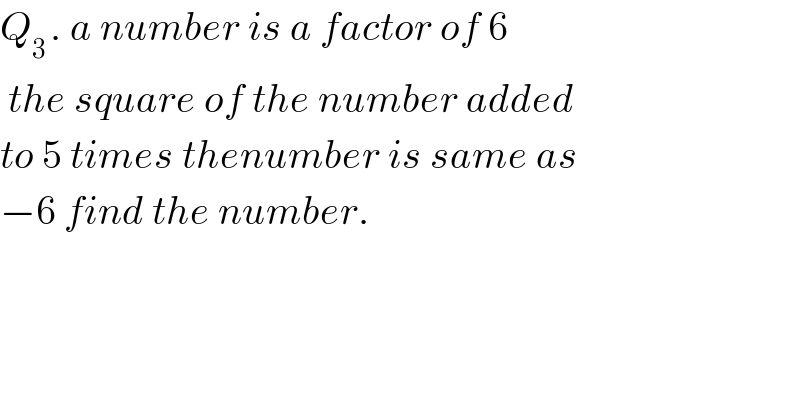
$${Q}_{\mathrm{3}\:} .\:{a}\:{number}\:{is}\:{a}\:{factor}\:{of}\:\mathrm{6} \\ $$$$\:{the}\:{square}\:{of}\:{the}\:{number}\:{added}\: \\ $$$${to}\:\mathrm{5}\:{times}\:{thenumber}\:{is}\:{same}\:{as} \\ $$$$−\mathrm{6}\:{find}\:{the}\:{number}. \\ $$
Answered by MJS last updated on 18/May/18

$${x}^{\mathrm{2}} +\mathrm{5}{x}=−\mathrm{6} \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{just}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{and}\:\mathrm{take}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{which} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{6} \\ $$
Answered by ajfour last updated on 18/May/18
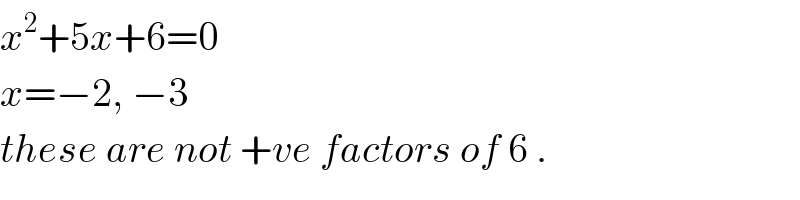
$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}=\mathrm{0} \\ $$$${x}=−\mathrm{2},\:−\mathrm{3} \\ $$$${these}\:{are}\:{not}\:+{ve}\:{factors}\:{of}\:\mathrm{6}\:. \\ $$
Commented by MJS last updated on 18/May/18
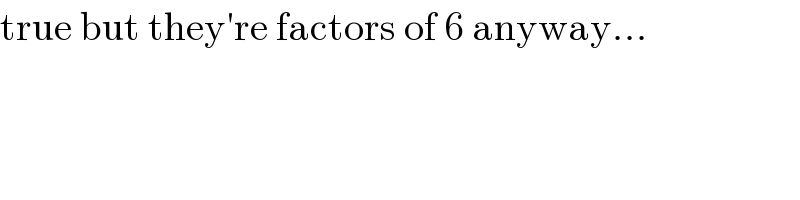
$$\mathrm{true}\:\mathrm{but}\:\mathrm{they}'\mathrm{re}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{6}\:\mathrm{anyway}... \\ $$
