
Question Number 212935 by MrGaster last updated on 27/Oct/24
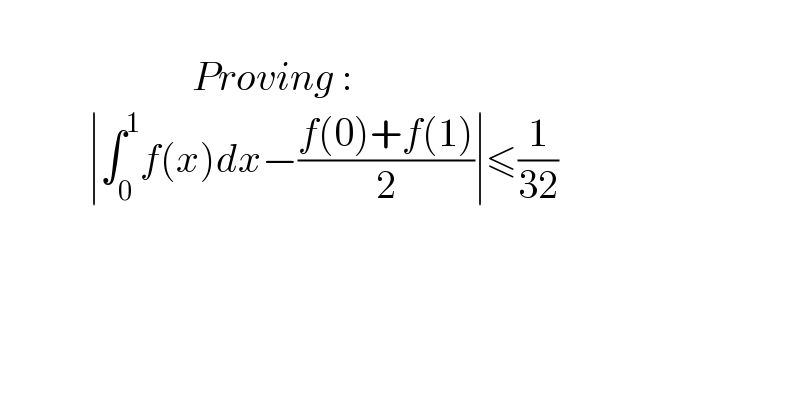
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Proving}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mid\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}−\frac{{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{1}\right)}{\mathrm{2}}\mid\leqslant\frac{\mathrm{1}}{\mathrm{32}} \\ $$$$ \\ $$
Answered by mehdee7396 last updated on 27/Oct/24
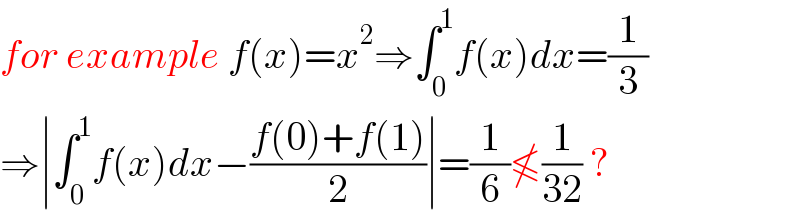
$${for}\:{example}\:{f}\left({x}\right)={x}^{\mathrm{2}} \Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\mid\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}−\frac{{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{1}\right)}{\mathrm{2}}\mid=\frac{\mathrm{1}}{\mathrm{6}}\nleqslant\frac{\mathrm{1}}{\mathrm{32}}\:? \\ $$
