
Question Number 216830 by MrGaster last updated on 22/Feb/25
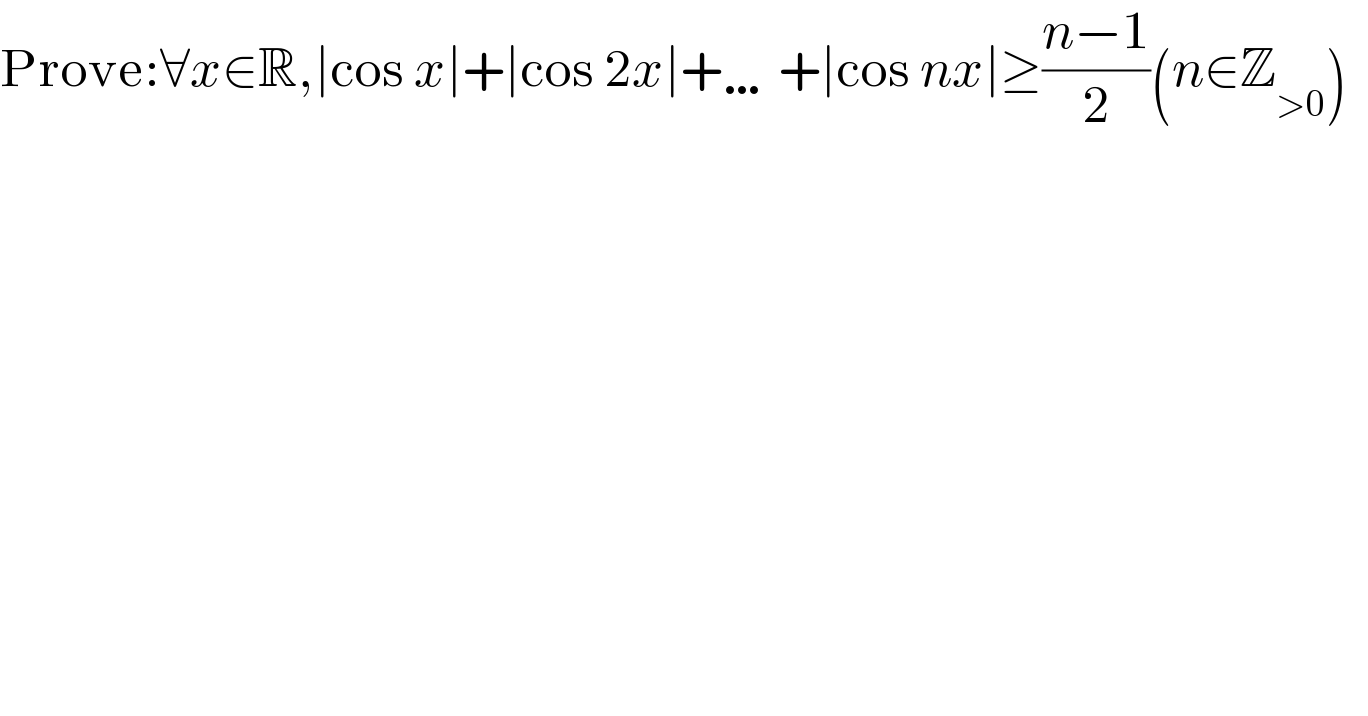
$$\mathrm{Prove}:\forall{x}\in\mathbb{R},\mid\mathrm{cos}\:{x}\mid+\mid\mathrm{cos}\:\mathrm{2}{x}\mid+\ldots+\mid\mathrm{cos}\:{nx}\mid\geq\frac{{n}−\mathrm{1}}{\mathrm{2}}\left({n}\in\mathbb{Z}_{>\mathrm{0}} \right)\:\: \\ $$
Commented by MathematicalUser2357 last updated on 25/Feb/25
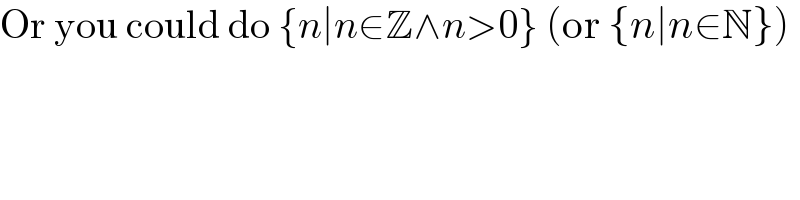
$$\mathrm{Or}\:\mathrm{you}\:\mathrm{could}\:\mathrm{do}\:\left\{{n}\mid{n}\in\mathbb{Z}\wedge{n}>\mathrm{0}\right\}\:\left(\mathrm{or}\:\left\{{n}\mid{n}\in\mathbb{N}\right\}\right) \\ $$
Answered by MrGaster last updated on 23/Feb/25
![Prove:Σ_(k=1) ^n ∣cos(kπ)∣≥((n−1)/2) (n ∈ Z_(>0) ) Let S_n (x)=Σ_(k=1) ^n ∣cos(kx)∣ ⇒S_n (x)=∣cos(x)∣+∣cos(2x)∣+…+∣cos(nx)∣ Consider T_n (x)=Σ_(k=1) ^n cos(kπ) =((sin(((nx)/2))cos((((n+1)x)/2)))/(sin((x/2)))) ⇒∣T_n (x)∣≤(1/(∣sin((x/2))∣)) Let U_n (x)=Σ_(k=1) ^n cos^2 (kπ) =(n/2)+(1/2)Σ_(k=1) ^n cos(2kx) =(n/2)+(1/2)(((sin(nx)cos((n+1)x))/(sin(x)))) ⇒U_n (x)≤(n/2)+(1/2) ∵ ∣cos(kx)∣≥cos^2 (kx) ⇒S_n (x)≥U_n (x) ⇒S_n (x)≥(n/2)−(1/2) ∴S_n (x)≥((n−1)/2) [Q.E.D]](Q216849.png)
$$\mathrm{Prove}:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mid\mathrm{cos}\left({k}\pi\right)\mid\geq\frac{{n}−\mathrm{1}}{\mathrm{2}}\:\left({n}\:\in\:\mathbb{Z}_{>\mathrm{0}} \right) \\ $$$$\mathrm{Let}\:{S}_{{n}} \left({x}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mid\mathrm{cos}\left({kx}\right)\mid \\ $$$$\Rightarrow{S}_{{n}} \left({x}\right)=\mid\mathrm{cos}\left({x}\right)\mid+\mid\mathrm{cos}\left(\mathrm{2}{x}\right)\mid+\ldots+\mid\mathrm{cos}\left({nx}\right)\mid \\ $$$$\mathrm{Consider}\:{T}_{{n}} \left({x}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\left({k}\pi\right) \\ $$$$=\frac{\mathrm{sin}\left(\frac{{nx}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\mid{T}_{{n}} \left({x}\right)\mid\leq\frac{\mathrm{1}}{\mid\mathrm{sin}\left(\frac{{x}}{\mathrm{2}}\right)\mid} \\ $$$$\mathrm{Let}\:{U}_{{n}} \left({x}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}^{\mathrm{2}} \left({k}\pi\right) \\ $$$$=\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\left(\mathrm{2}{kx}\right) \\ $$$$=\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{sin}\left({nx}\right)\mathrm{cos}\left(\left({n}+\mathrm{1}\right){x}\right)}{\mathrm{sin}\left({x}\right)}\right) \\ $$$$\Rightarrow{U}_{{n}} \left({x}\right)\leq\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\because\:\mid\mathrm{cos}\left({kx}\right)\mid\geq\mathrm{cos}^{\mathrm{2}} \left({kx}\right) \\ $$$$\Rightarrow{S}_{{n}} \left({x}\right)\geq{U}_{{n}} \left({x}\right) \\ $$$$\Rightarrow{S}_{{n}} \left({x}\right)\geq\frac{{n}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\therefore{S}_{{n}} \left({x}\right)\geq\frac{{n}−\mathrm{1}}{\mathrm{2}} \\ $$$$\left[\mathrm{Q}.\mathrm{E}.\mathrm{D}\right] \\ $$
