
Question Number 62169 by Tawa1 last updated on 16/Jun/19
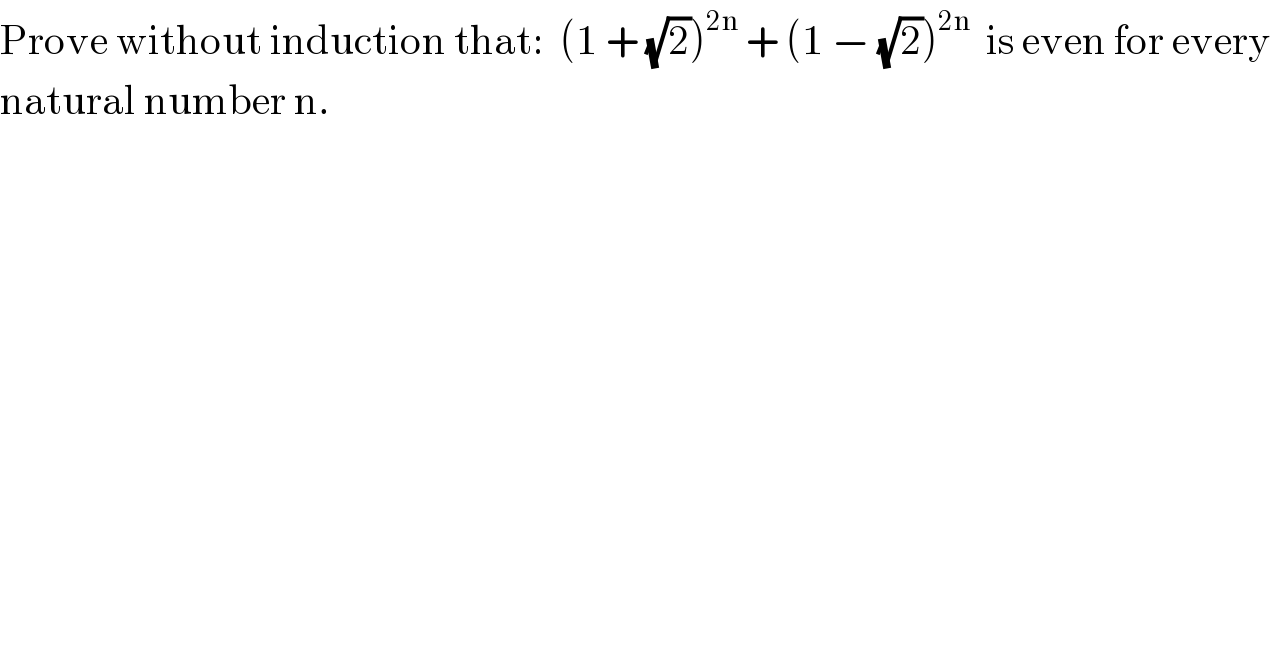
$$\mathrm{Prove}\:\mathrm{without}\:\mathrm{induction}\:\mathrm{that}:\:\:\left(\mathrm{1}\:+\:\sqrt{\mathrm{2}}\right)^{\mathrm{2n}} \:+\:\left(\mathrm{1}\:−\:\sqrt{\mathrm{2}}\right)^{\mathrm{2n}} \:\:\mathrm{is}\:\mathrm{even}\:\mathrm{for}\:\mathrm{every} \\ $$$$\mathrm{natural}\:\mathrm{number}\:\mathrm{n}.\:\:\: \\ $$
Answered by ajfour last updated on 16/Jun/19
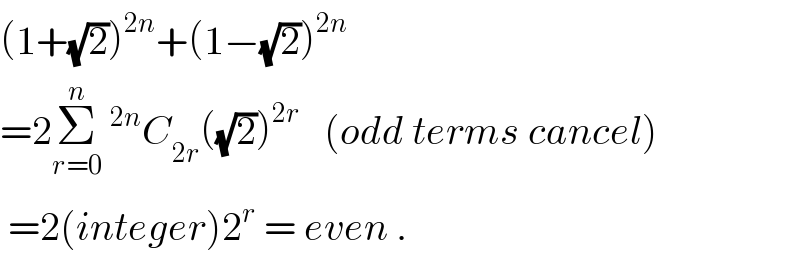
$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}{n}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}{n}} \\ $$$$=\mathrm{2}\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{\mathrm{2}{n}} {C}_{\mathrm{2}{r}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}{r}} \:\:\:\left({odd}\:{terms}\:{cancel}\right) \\ $$$$\:=\mathrm{2}\left({integer}\right)\mathrm{2}^{{r}} \:=\:{even}\:. \\ $$
Commented by mr W last updated on 16/Jun/19
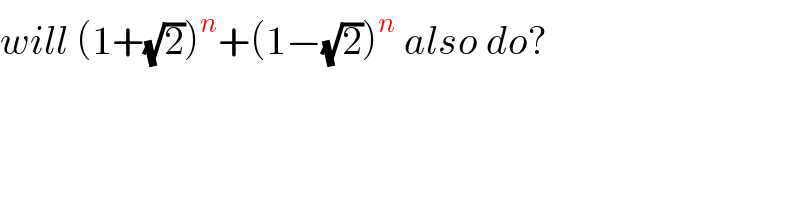
$${will}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{n}} \:{also}\:{do}? \\ $$
Commented by Tawa1 last updated on 16/Jun/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
