
Question Number 164162 by Zaynal last updated on 15/Jan/22
![Prove the; (tan 𝛂 + ((cos 𝛂)/(1 + sin 𝛂))) sin 𝛂 = 𝛂 ^([Z.A])](Q164162.png)
$$\mathrm{Prove}\:\mathrm{the}; \\ $$$$\left(\boldsymbol{{tan}}\:\boldsymbol{\alpha}\:+\:\frac{\boldsymbol{{cos}}\:\boldsymbol{\alpha}}{\mathrm{1}\:+\:\boldsymbol{{sin}}\:\boldsymbol{\alpha}}\right)\:\boldsymbol{{sin}}\:\boldsymbol{\alpha}\:=\:\boldsymbol{\alpha} \\ $$$$\:^{\left[\mathrm{Z}.\mathrm{A}\right]} \\ $$
Commented by som(math1967) last updated on 15/Jan/22
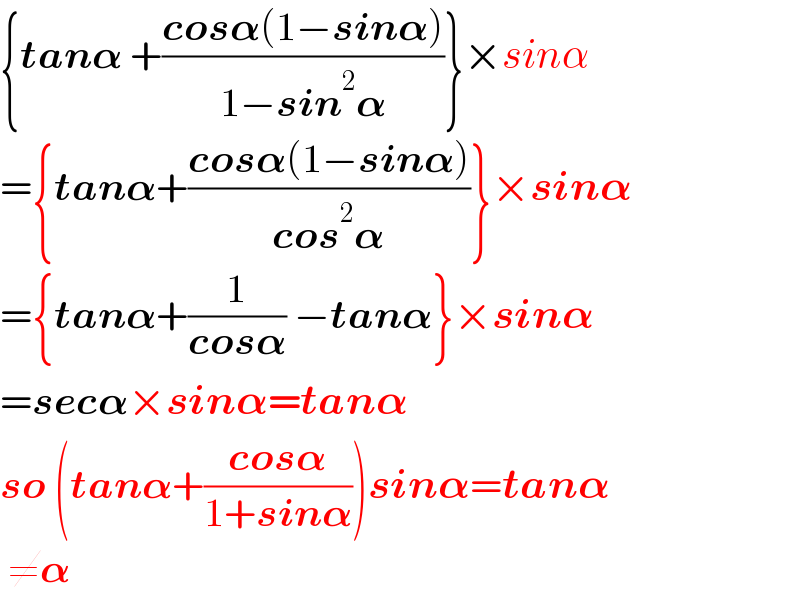
$$\left\{\boldsymbol{{tan}\alpha}\:+\frac{\boldsymbol{{cos}\alpha}\left(\mathrm{1}−\boldsymbol{{sin}\alpha}\right)}{\mathrm{1}−\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{\alpha}}\right\}×{sin}\alpha \\ $$$$=\left\{\boldsymbol{{tan}\alpha}+\frac{\boldsymbol{{cos}\alpha}\left(\mathrm{1}−\boldsymbol{{sin}\alpha}\right)}{\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\alpha}}\right\}×\boldsymbol{{sin}\alpha} \\ $$$$=\left\{\boldsymbol{{tan}\alpha}+\frac{\mathrm{1}}{\boldsymbol{{cos}\alpha}}\:−\boldsymbol{{tan}\alpha}\right\}×\boldsymbol{{sin}\alpha} \\ $$$$=\boldsymbol{{sec}\alpha}×\boldsymbol{{sin}\alpha}=\boldsymbol{{tan}\alpha} \\ $$$$\boldsymbol{{so}}\:\left(\boldsymbol{{tan}\alpha}+\frac{\boldsymbol{{cos}\alpha}}{\mathrm{1}+\boldsymbol{{sin}\alpha}}\right)\boldsymbol{{sin}\alpha}=\boldsymbol{{tan}\alpha} \\ $$$$\:\neq\boldsymbol{\alpha} \\ $$
Commented by Zaynal last updated on 15/Jan/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}..,\: \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{tan}\:\mathrm{apha} \\ $$
Commented by cortano1 last updated on 15/Jan/22

Commented by som(math1967) last updated on 15/Jan/22
$${sorry}\:{typo}\:{i}\:{corrected} \\ $$
Commented by Zaynal last updated on 15/Jan/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{very}\:\mathrm{good}. \\ $$
