
Question Number 9086 by tawakalitu last updated on 17/Nov/16
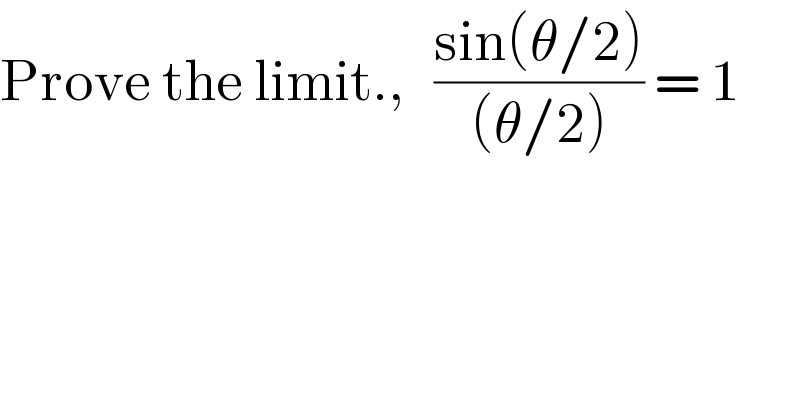
$$\mathrm{Prove}\:\mathrm{the}\:\mathrm{limit}.,\:\:\:\frac{\mathrm{sin}\left(\theta/\mathrm{2}\right)}{\left(\theta/\mathrm{2}\right)}\:=\:\mathrm{1} \\ $$
Commented by 123456 last updated on 17/Nov/16
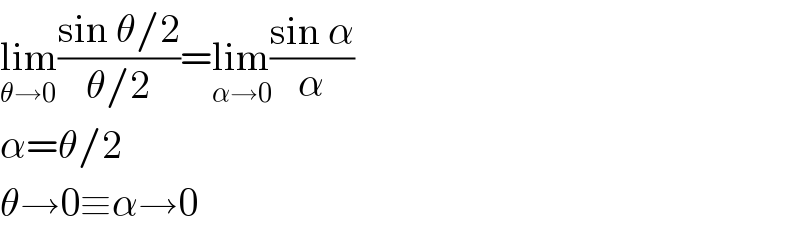
$$\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\theta/\mathrm{2}}{\theta/\mathrm{2}}=\underset{\alpha\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\alpha}{\alpha} \\ $$$$\alpha=\theta/\mathrm{2} \\ $$$$\theta\rightarrow\mathrm{0}\equiv\alpha\rightarrow\mathrm{0} \\ $$
Commented by 123456 last updated on 17/Nov/16
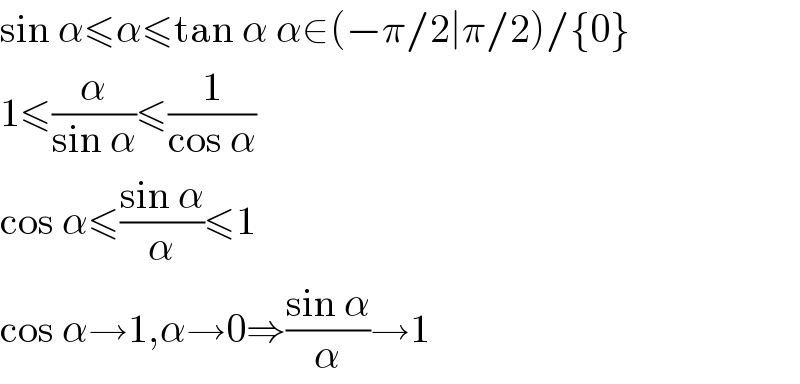
$$\mathrm{sin}\:\alpha\leqslant\alpha\leqslant\mathrm{tan}\:\alpha\:\alpha\in\left(−\pi/\mathrm{2}\mid\pi/\mathrm{2}\right)/\left\{\mathrm{0}\right\} \\ $$$$\mathrm{1}\leqslant\frac{\alpha}{\mathrm{sin}\:\alpha}\leqslant\frac{\mathrm{1}}{\mathrm{cos}\:\alpha} \\ $$$$\mathrm{cos}\:\alpha\leqslant\frac{\mathrm{sin}\:\alpha}{\alpha}\leqslant\mathrm{1} \\ $$$$\mathrm{cos}\:\alpha\rightarrow\mathrm{1},\alpha\rightarrow\mathrm{0}\Rightarrow\frac{\mathrm{sin}\:\alpha}{\alpha}\rightarrow\mathrm{1} \\ $$
