
Question Number 5603 by sanusihammed last updated on 22/May/16
![Prove the identity log_(a/b) x = ((log_a x log_b x)/(log_b x − log_a x)) From the Right hand side ((log_a x log_b x)/(log_b x − log_a x)) Using... log_n m = ((logm)/(logn)) = ((((logx)/(loga)) × ((logx)/(logb)))/( ((logx)/(logb)) − ((logx)/(loga)))) = ((((logx)^2 )/(loga logb))/((logalogx − logb logx)/(loga logb ))) = (((logx)^2 )/(loga logb)) × ((loga logb)/(logalogx − logblogx)) = (((logx)^2 )/(logalogx − logblogx)) = (((logx)^2 )/(logx(loga − logb))) = ((logx)/(loga − logb )) = ((logx)/(log(a/b))) Using... log_n m = ((logm)/(logn)) = log_(a/b) x [Left Hand Side] PROVED THANKS SO MUCH YOZII](Q5603.png)
$${Prove}\:{the}\:{identity} \\ $$$$ \\ $$$${log}_{\frac{{a}}{{b}}} {x}\:\:=\:\:\frac{{log}_{{a}} {x}\:{log}_{{b}} {x}}{{log}_{{b}} {x}\:−\:{log}_{{a}} {x}} \\ $$$$ \\ $$$${From}\:{the}\:{Right}\:{hand}\:{side}\: \\ $$$$ \\ $$$$\frac{{log}_{{a}} {x}\:{log}_{{b}} {x}}{{log}_{{b}} {x}\:−\:{log}_{{a}} {x}} \\ $$$$ \\ $$$${Using}...\:{log}_{{n}} {m}\:=\:\frac{{logm}}{{logn}} \\ $$$$ \\ $$$$=\:\frac{\frac{{logx}}{{loga}}\:×\:\frac{{logx}}{{logb}}}{\:\frac{{logx}}{{logb}}\:−\:\frac{{logx}}{{loga}}} \\ $$$$ \\ $$$$=\:\frac{\frac{\left({logx}\right)^{\mathrm{2}} }{{loga}\:{logb}}}{\frac{{logalogx}\:−\:{logb}\:{logx}}{{loga}\:{logb}\:}} \\ $$$$ \\ $$$$=\:\frac{\left({logx}\right)^{\mathrm{2}} }{{loga}\:{logb}}\:×\:\frac{{loga}\:{logb}}{{logalogx}\:−\:{logblogx}} \\ $$$$ \\ $$$$=\:\frac{\left({logx}\right)^{\mathrm{2}} }{{logalogx}\:−\:{logblogx}} \\ $$$$ \\ $$$$=\:\frac{\left({logx}\right)^{\mathrm{2}} }{{logx}\left({loga}\:−\:{logb}\right)} \\ $$$$ \\ $$$$=\:\frac{{logx}}{{loga}\:−\:{logb}\:} \\ $$$$ \\ $$$$=\:\frac{{logx}}{{log}\frac{{a}}{{b}}} \\ $$$$ \\ $$$${Using}...\:{log}_{{n}} {m}\:=\:\frac{{logm}}{{logn}} \\ $$$$ \\ $$$$=\:{log}_{\frac{{a}}{{b}}} {x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{Left}\:{Hand}\:{Side}\right] \\ $$$$ \\ $$$${PROVED} \\ $$$$ \\ $$$$ \\ $$$${THANKS}\:{SO}\:{MUCH}\:{YOZII} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzii last updated on 21/May/16
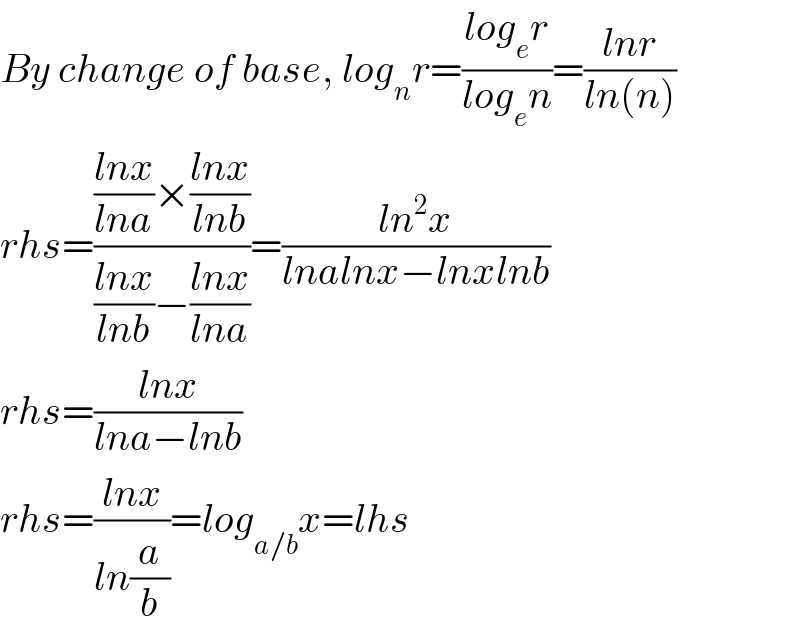
$${By}\:{change}\:{of}\:{base},\:{log}_{{n}} {r}=\frac{{log}_{{e}} {r}}{{log}_{{e}} {n}}=\frac{{lnr}}{{ln}\left({n}\right)} \\ $$$${rhs}=\frac{\frac{{lnx}}{{lna}}×\frac{{lnx}}{{lnb}}}{\frac{{lnx}}{{lnb}}−\frac{{lnx}}{{lna}}}=\frac{{ln}^{\mathrm{2}} {x}}{{lnalnx}−{lnxlnb}} \\ $$$${rhs}=\frac{{lnx}}{{lna}−{lnb}} \\ $$$${rhs}=\frac{{lnx}}{{ln}\frac{{a}}{{b}}}={log}_{{a}/{b}} {x}={lhs} \\ $$
Commented by sanusihammed last updated on 22/May/16

$${Thanks} \\ $$
