Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 140056 by Ndala last updated on 03/May/21

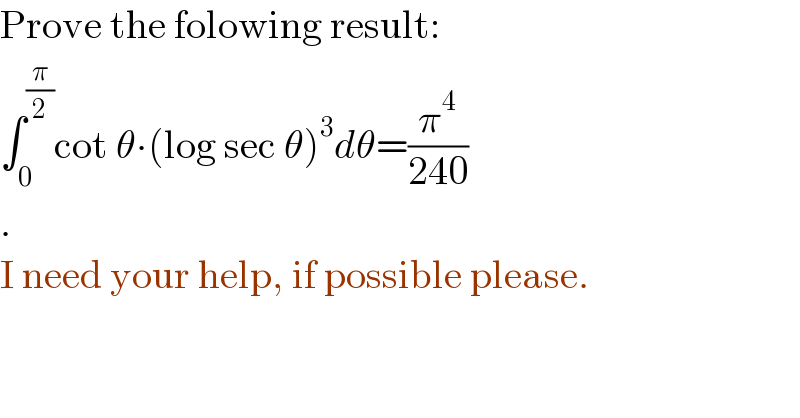
Prove the folowing result: ∫_0 ^(π/2) cot θ∙(log sec θ)^3 dθ=(π^4 /(240)) . I need your help, if possible please.

$$\mathrm{Prove}\:\mathrm{the}\:\mathrm{folowing}\:\mathrm{result}: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cot}\:\theta\centerdot\left(\mathrm{log}\:\mathrm{sec}\:\theta\right)^{\mathrm{3}} {d}\theta=\frac{\pi^{\mathrm{4}} }{\mathrm{240}} \\ $$$$. \\ $$$$\mathrm{I}\:\mathrm{need}\:\mathrm{your}\:\mathrm{help},\:\mathrm{if}\:\mathrm{possible}\:\mathrm{please}. \\ $$

Answered by Ar Brandon last updated on 04/May/21

∫_0 ^(π/2) cotθ(ln secθ)^3 dθ=−∫_0 ^(π/2) sin^(−1) θcosθ∙ln^3 cosθdθ β(m,n)=2∫_0 ^(π/2) sin^(2m−1) θcos^(2n−1) θdθ=((Γ(m)Γ(n))/(Γ(m+n))) lnβ(m,n)=lnΓ(m)+lnΓ(n)−lnΓ(m+n) ((β ′(m,n))/(β(m,n)))=ψ(n)−ψ(m+n) β′′(m,n)=β(m,n)[ψ′(n)−ψ′(m+n)]+β′(m,n)[ψ(n)−ψ(m+n)] β′′′(m,n)=β(m,n)[ψ′′(n)−ψ′′(m+n)]+β′(m,n)[ψ′(n)−ψ′(m+n)] +β′′(m,n)[ψ(n)−ψ(m+n)]+β′(m,n)[ψ′(n)−ψ′(m+n)]

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cot}\theta\left(\mathrm{ln}\:\mathrm{sec}\theta\right)^{\mathrm{3}} \mathrm{d}\theta=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{−\mathrm{1}} \theta\mathrm{cos}\theta\centerdot\mathrm{ln}^{\mathrm{3}} \mathrm{cos}\theta\mathrm{d}\theta \\ $$$$\beta\left(\mathrm{m},\mathrm{n}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2m}−\mathrm{1}} \theta\mathrm{cos}^{\mathrm{2n}−\mathrm{1}} \theta\mathrm{d}\theta=\frac{\Gamma\left(\mathrm{m}\right)\Gamma\left(\mathrm{n}\right)}{\Gamma\left(\mathrm{m}+\mathrm{n}\right)} \\ $$$$\mathrm{ln}\beta\left(\mathrm{m},\mathrm{n}\right)=\mathrm{ln}\Gamma\left(\mathrm{m}\right)+\mathrm{ln}\Gamma\left(\mathrm{n}\right)−\mathrm{ln}\Gamma\left(\mathrm{m}+\mathrm{n}\right) \\ $$$$\frac{\beta\:'\left(\mathrm{m},\mathrm{n}\right)}{\beta\left(\mathrm{m},\mathrm{n}\right)}=\psi\left(\mathrm{n}\right)−\psi\left(\mathrm{m}+\mathrm{n}\right) \\ $$$$\beta''\left(\mathrm{m},\mathrm{n}\right)=\beta\left(\mathrm{m},\mathrm{n}\right)\left[\psi'\left(\mathrm{n}\right)−\psi'\left(\mathrm{m}+\mathrm{n}\right)\right]+\beta'\left(\mathrm{m},\mathrm{n}\right)\left[\psi\left(\mathrm{n}\right)−\psi\left(\mathrm{m}+\mathrm{n}\right)\right] \\ $$$$\beta'''\left(\mathrm{m},\mathrm{n}\right)=\beta\left(\mathrm{m},\mathrm{n}\right)\left[\psi''\left(\mathrm{n}\right)−\psi''\left(\mathrm{m}+\mathrm{n}\right)\right]+\beta'\left(\mathrm{m},\mathrm{n}\right)\left[\psi'\left(\mathrm{n}\right)−\psi'\left(\mathrm{m}+\mathrm{n}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\beta''\left(\mathrm{m},\mathrm{n}\right)\left[\psi\left(\mathrm{n}\right)−\psi\left(\mathrm{m}+\mathrm{n}\right)\right]+\beta'\left(\mathrm{m},\mathrm{n}\right)\left[\psi'\left(\mathrm{n}\right)−\psi'\left(\mathrm{m}+\mathrm{n}\right)\right] \\ $$

Commented by Ndala last updated on 07/May/21

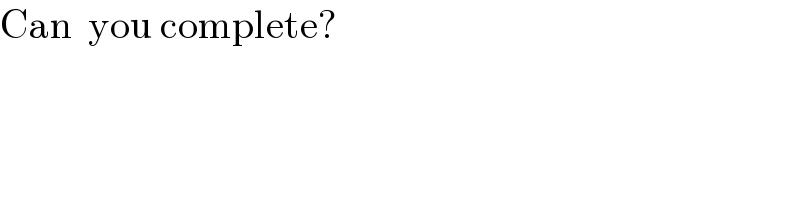
Can you complete?

$$\mathrm{Can}\:\:\mathrm{you}\:\mathrm{complete}? \\ $$

Answered by qaz last updated on 07/May/21

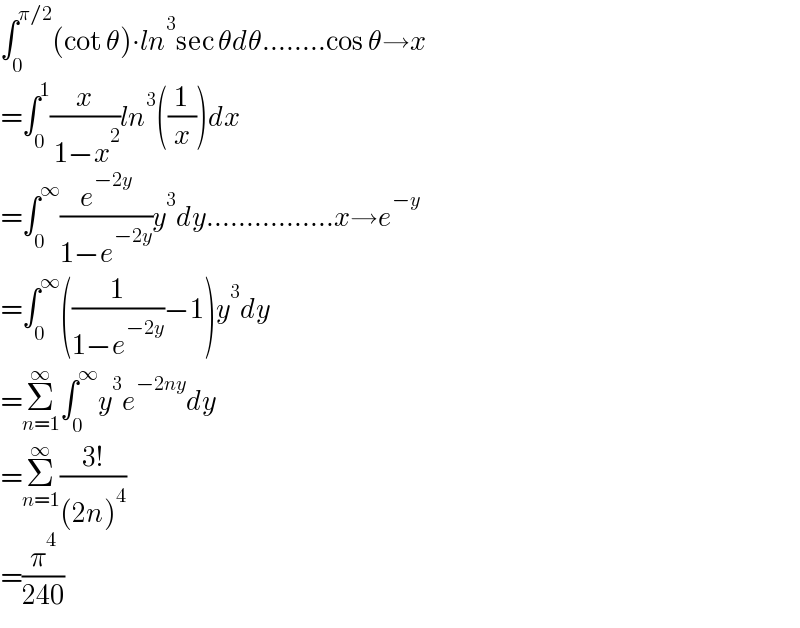
∫_0 ^(π/2) (cot θ)∙ln^3 sec θdθ........cos θ→x =∫_0 ^1 (x/( 1−x^2 ))ln^3 ((1/x))dx =∫_0 ^∞ (e^(−2y) /(1−e^(−2y) ))y^3 dy................x→e^(−y) =∫_0 ^∞ ((1/(1−e^(−2y) ))−1)y^3 dy =Σ_(n=1) ^∞ ∫_0 ^∞ y^3 e^(−2ny) dy =Σ_(n=1) ^∞ ((3!)/((2n)^4 )) =(π^4 /(240))

$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{cot}\:\theta\right)\centerdot{ln}^{\mathrm{3}} \mathrm{sec}\:\theta{d}\theta........\mathrm{cos}\:\theta\rightarrow{x} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\:\mathrm{1}−{x}^{\mathrm{2}} }{ln}^{\mathrm{3}} \left(\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{2}{y}} }{\mathrm{1}−{e}^{−\mathrm{2}{y}} }{y}^{\mathrm{3}} {dy}................{x}\rightarrow{e}^{−{y}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{1}−{e}^{−\mathrm{2}{y}} }−\mathrm{1}\right){y}^{\mathrm{3}} {dy} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {y}^{\mathrm{3}} {e}^{−\mathrm{2}{ny}} {dy} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}!}{\left(\mathrm{2}{n}\right)^{\mathrm{4}} } \\ $$$$=\frac{\pi^{\mathrm{4}} }{\mathrm{240}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com