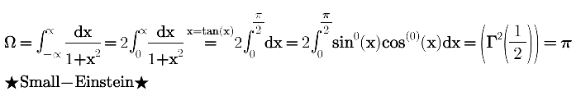Question Number 164163 by Zaynal last updated on 15/Jan/22
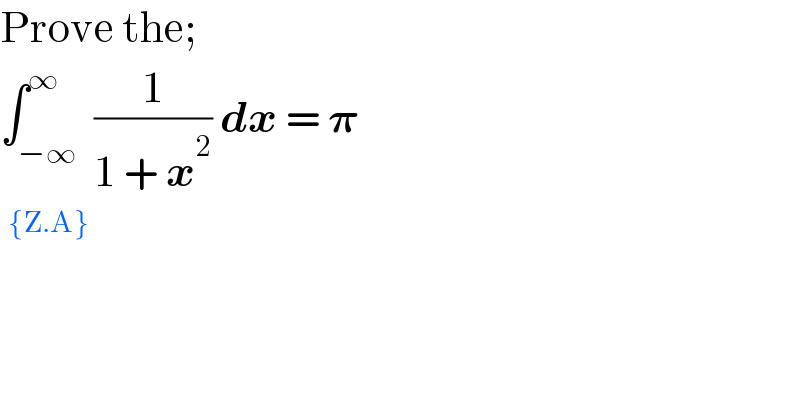
$$\mathrm{Prove}\:\mathrm{the}; \\ $$$$\int_{β\infty} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}\:+\:\boldsymbol{{x}}^{\mathrm{2}} }\:\boldsymbol{{dx}}\:=\:\boldsymbol{\pi} \\ $$$$\:^{\left\{\mathrm{Z}.\mathrm{A}\right\}} \\ $$
Answered by mathmax by abdo last updated on 15/Jan/22
![β«_(ββ) ^(+β) (dx/(1+x^2 ))=lim_(ΞΎβ+β) β«_(βΞΎ) ^ΞΎ (dx/(1+x^2 ))=lim_(ΞΎβ+β) [arctanx]_(βΞΎ) ^ΞΎ =lim_(ΞΎβ+β) 2arctanΞΎ =2.(Ο/2)=Ο or β«_(ββ) ^(+β) (dx/(1+x^2 ))=_(x=tanΞΈ) β«_(β(Ο/2)) ^(Ο/2) ((1+tan^2 ΞΈ)/(1+tan^2 ΞΈ))dΞΈ =β«_(β(Ο/2)) ^(Ο/2) dΞΈ =Ο](Q164164.png)
$$\int_{β\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\mathrm{lim}_{\xi\rightarrow+\infty} \:\:\int_{β\xi} ^{\xi} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\mathrm{lim}_{\xi\rightarrow+\infty} \left[\mathrm{arctanx}\right]_{β\xi} ^{\xi} \\ $$$$=\mathrm{lim}_{\xi\rightarrow+\infty} \mathrm{2arctan}\xi\:=\mathrm{2}.\frac{\pi}{\mathrm{2}}=\pi \\ $$$$\mathrm{or} \\ $$$$\int_{β\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\int_{β\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\mathrm{d}\theta\:=\int_{β\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{d}\theta\:=\pi \\ $$
Commented by Zaynal last updated on 15/Jan/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{very}\:\mathrm{good}\: \\ $$
Commented by Mathspace last updated on 15/Jan/22
$${you}\:{are}\:{welcome} \\ $$
Answered by smallEinstein last updated on 16/Jan/22
