
Question Number 19350 by Tinkutara last updated on 10/Aug/17
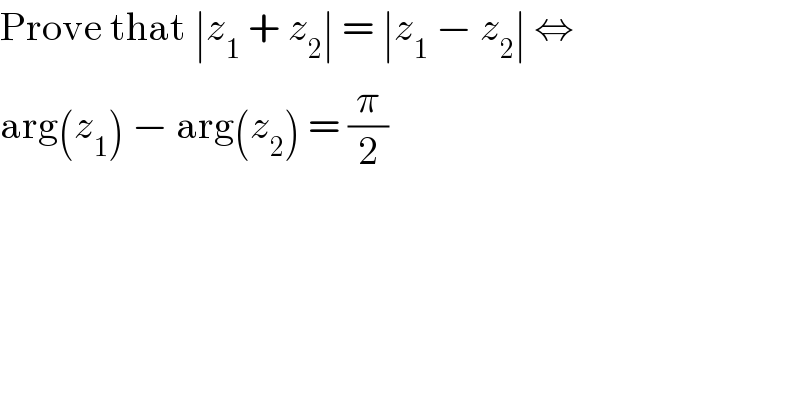
$$\mathrm{Prove}\:\mathrm{that}\:\mid{z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \mid\:=\:\mid{z}_{\mathrm{1}} \:−\:{z}_{\mathrm{2}} \mid\:\Leftrightarrow \\ $$$$\mathrm{arg}\left({z}_{\mathrm{1}} \right)\:−\:\mathrm{arg}\left({z}_{\mathrm{2}} \right)\:=\:\frac{\pi}{\mathrm{2}} \\ $$
Answered by ajfour last updated on 10/Aug/17
![⇒ ∣z_1 +z_2 ∣^2 =∣z_1 −z_2 ∣^2 z_1 ^2 +z_2 ^2 +2Re(z_1 z_2 ^� )=z_1 ^2 +z_2 ^2 −2Re(z_1 z_2 ^� ) ⇒ Re(z_1 z_2 ^� )=0 Re[(x_1 +iy_1 )(x_2 −iy_2 )]=0 ⇒ x_1 x_2 =−y_1 y_2 ⇒ (y_2 /x_2 ) =−(x_1 /y_1 ) ⇒tan [arg(z_2 )]=−(1/(tan [arg(z_1 )])) ⇒ tan θ_1 tan θ_2 +1=0 and as tan (θ_1 −θ_2 )=((tan θ_1 −tan θ_2 )/(1+tan θ_1 tan θ_2 )) ⇒ θ_1 −θ_2 =(π/2) arg(z_1 )−arg(z_2 )= (π/2) .](Q19371.png)
$$\Rightarrow\:\mid\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} \mid^{\mathrm{2}} =\mid\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \mid^{\mathrm{2}} \\ $$$$\mathrm{z}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{z}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2Re}\left(\mathrm{z}_{\mathrm{1}} \bar {\mathrm{z}}_{\mathrm{2}} \right)=\mathrm{z}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{z}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2Re}\left(\mathrm{z}_{\mathrm{1}} \bar {\mathrm{z}}_{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\mathrm{Re}\left(\mathrm{z}_{\mathrm{1}} \bar {\mathrm{z}}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\:\:\mathrm{Re}\left[\left(\mathrm{x}_{\mathrm{1}} +\mathrm{iy}_{\mathrm{1}} \right)\left(\mathrm{x}_{\mathrm{2}} −\mathrm{iy}_{\mathrm{2}} \right)\right]=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} =−\mathrm{y}_{\mathrm{1}} \mathrm{y}_{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{y}_{\mathrm{2}} }{\mathrm{x}_{\mathrm{2}} }\:=−\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{y}_{\mathrm{1}} } \\ $$$$\Rightarrow\mathrm{tan}\:\left[\mathrm{arg}\left(\mathrm{z}_{\mathrm{2}} \right)\right]=−\frac{\mathrm{1}}{\mathrm{tan}\:\left[\mathrm{arg}\left(\mathrm{z}_{\mathrm{1}} \right)\right]} \\ $$$$\Rightarrow\:\mathrm{tan}\:\theta_{\mathrm{1}} \mathrm{tan}\:\theta_{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{as}\:\mathrm{tan}\:\left(\theta_{\mathrm{1}} −\theta_{\mathrm{2}} \right)=\frac{\mathrm{tan}\:\theta_{\mathrm{1}} −\mathrm{tan}\:\theta_{\mathrm{2}} }{\mathrm{1}+\mathrm{tan}\:\theta_{\mathrm{1}} \mathrm{tan}\:\theta_{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\theta_{\mathrm{1}} −\theta_{\mathrm{2}} =\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{arg}\left(\mathrm{z}_{\mathrm{1}} \right)−\mathrm{arg}\left(\mathrm{z}_{\mathrm{2}} \right)=\:\frac{\pi}{\mathrm{2}}\:.\:\:\: \\ $$
Commented by Tinkutara last updated on 10/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
