
Question Number 38059 by suryavi last updated on 21/Jun/18
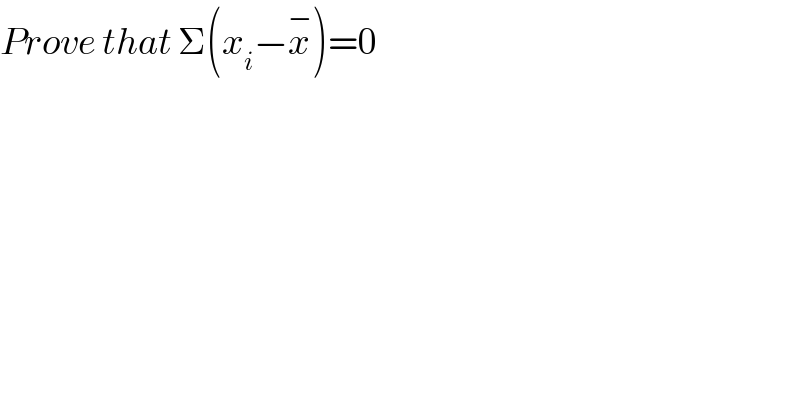
$${Prove}\:{that}\:\Sigma\left({x}_{{i}} −\overset{−} {{x}}\right)=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jun/18
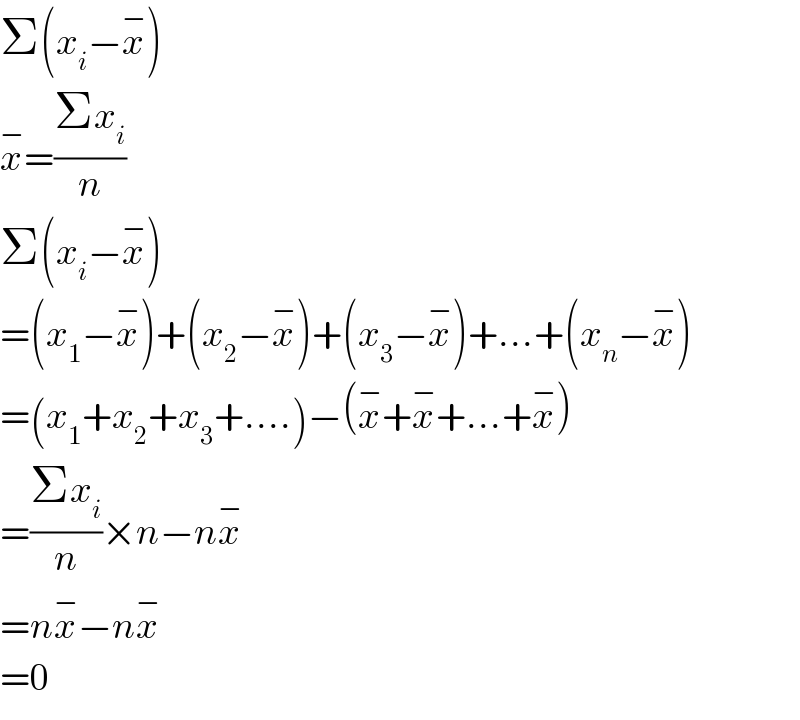
$$\Sigma\left({x}_{{i}} −\overset{−} {{x}}\right) \\ $$$$\overset{−} {{x}}=\frac{\Sigma{x}_{{i}} }{{n}} \\ $$$$\Sigma\left({x}_{{i}} −\overset{−} {{x}}\right) \\ $$$$=\left({x}_{\mathrm{1}} −\overset{−} {{x}}\right)+\left({x}_{\mathrm{2}} −\overset{−} {{x}}\right)+\left({x}_{\mathrm{3}} −\overset{−} {{x}}\right)+...+\left({x}_{{n}} −\overset{−} {{x}}\right) \\ $$$$=\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +....\right)−\left(\overset{−} {{x}}+\overset{−} {{x}}+...+\overset{−} {{x}}\right) \\ $$$$=\frac{\Sigma{x}_{{i}} }{{n}}×{n}−{n}\overset{−} {{x}} \\ $$$$={n}\overset{−} {{x}}−{n}\overset{−} {{x}} \\ $$$$=\mathrm{0} \\ $$
