
Question Number 196650 by CrispyXYZ last updated on 28/Aug/23
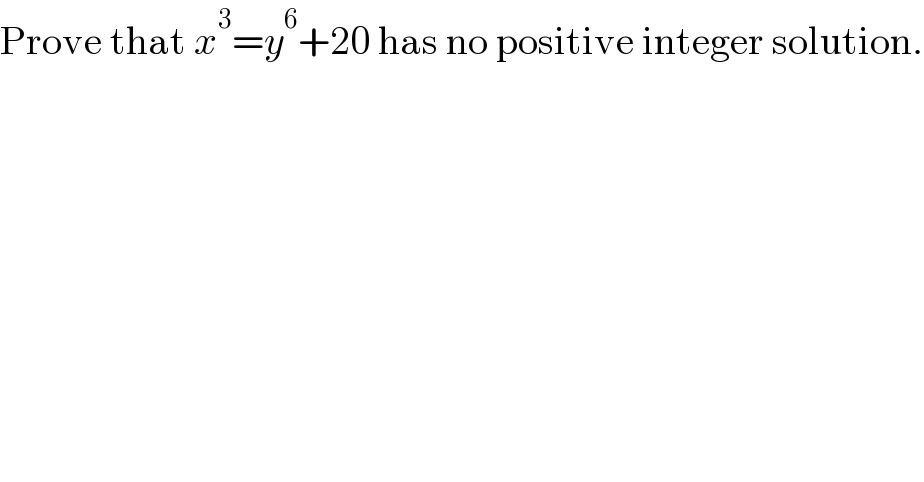
$$\mathrm{Prove}\:\mathrm{that}\:{x}^{\mathrm{3}} ={y}^{\mathrm{6}} +\mathrm{20}\:\mathrm{has}\:\mathrm{no}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{solution}. \\ $$
Answered by deleteduser1 last updated on 28/Aug/23
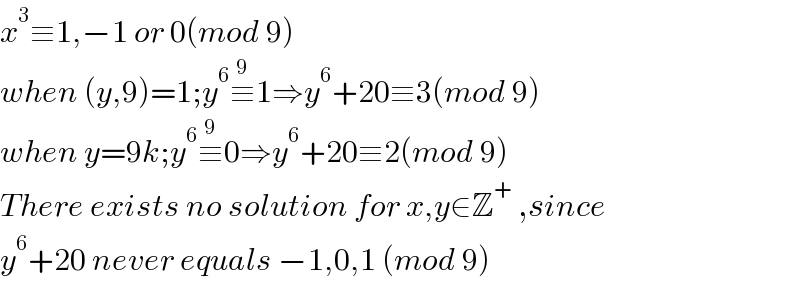
$${x}^{\mathrm{3}} \equiv\mathrm{1},−\mathrm{1}\:{or}\:\mathrm{0}\left({mod}\:\mathrm{9}\right) \\ $$$${when}\:\left({y},\mathrm{9}\right)=\mathrm{1};{y}^{\mathrm{6}} \overset{\mathrm{9}} {\equiv}\mathrm{1}\Rightarrow{y}^{\mathrm{6}} +\mathrm{20}\equiv\mathrm{3}\left({mod}\:\mathrm{9}\right) \\ $$$${when}\:{y}=\mathrm{9}{k};{y}^{\mathrm{6}} \overset{\mathrm{9}} {\equiv}\mathrm{0}\Rightarrow{y}^{\mathrm{6}} +\mathrm{20}\equiv\mathrm{2}\left({mod}\:\mathrm{9}\right) \\ $$$${There}\:{exists}\:{no}\:{solution}\:{for}\:{x},{y}\in\mathbb{Z}^{+} \:,{since}\: \\ $$$${y}^{\mathrm{6}} +\mathrm{20}\:{never}\:{equals}\:−\mathrm{1},\mathrm{0},\mathrm{1}\:\left({mod}\:\mathrm{9}\right) \\ $$
Answered by MM42 last updated on 29/Aug/23
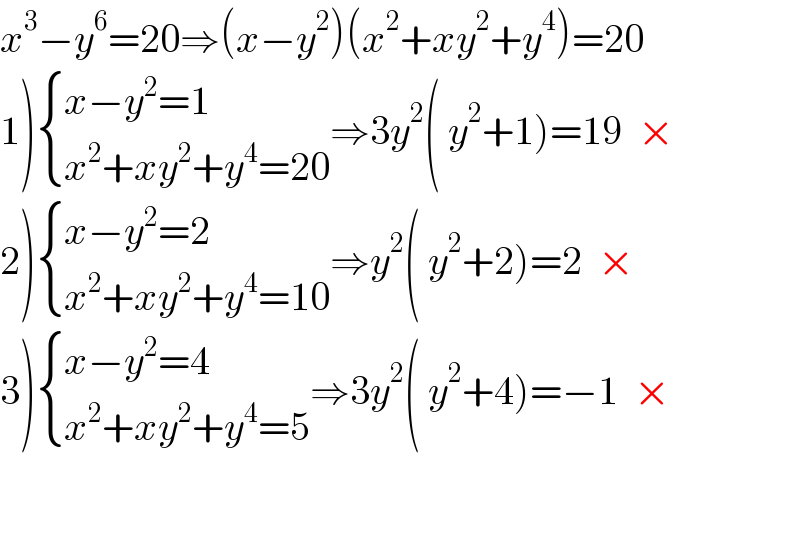
$${x}^{\mathrm{3}} −{y}^{\mathrm{6}} =\mathrm{20}\Rightarrow\left({x}−{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{xy}^{\mathrm{2}} +{y}^{\mathrm{4}} \right)=\mathrm{20} \\ $$$$\left.\mathrm{1}\right)\begin{cases}{{x}−{y}^{\mathrm{2}} =\mathrm{1}}\\{{x}^{\mathrm{2}} +{xy}^{\mathrm{2}} +{y}^{\mathrm{4}} =\mathrm{20}}\end{cases}\Rightarrow\mathrm{3}{y}^{\mathrm{2}} \left(\:{y}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{19}\:\:× \\ $$$$\left.\mathrm{2}\right)\begin{cases}{{x}−{y}^{\mathrm{2}} =\mathrm{2}}\\{{x}^{\mathrm{2}} +{xy}^{\mathrm{2}} +{y}^{\mathrm{4}} =\mathrm{10}}\end{cases}\Rightarrow{y}^{\mathrm{2}} \left(\:{y}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{2}\:\:× \\ $$$$\left.\mathrm{3}\right)\begin{cases}{{x}−{y}^{\mathrm{2}} =\mathrm{4}}\\{{x}^{\mathrm{2}} +{xy}^{\mathrm{2}} +{y}^{\mathrm{4}} =\mathrm{5}}\end{cases}\Rightarrow\mathrm{3}{y}^{\mathrm{2}} \left(\:{y}^{\mathrm{2}} +\mathrm{4}\right)=−\mathrm{1}\:\:× \\ $$$$ \\ $$$$ \\ $$
