
Question Number 195157 by Erico last updated on 25/Jul/23
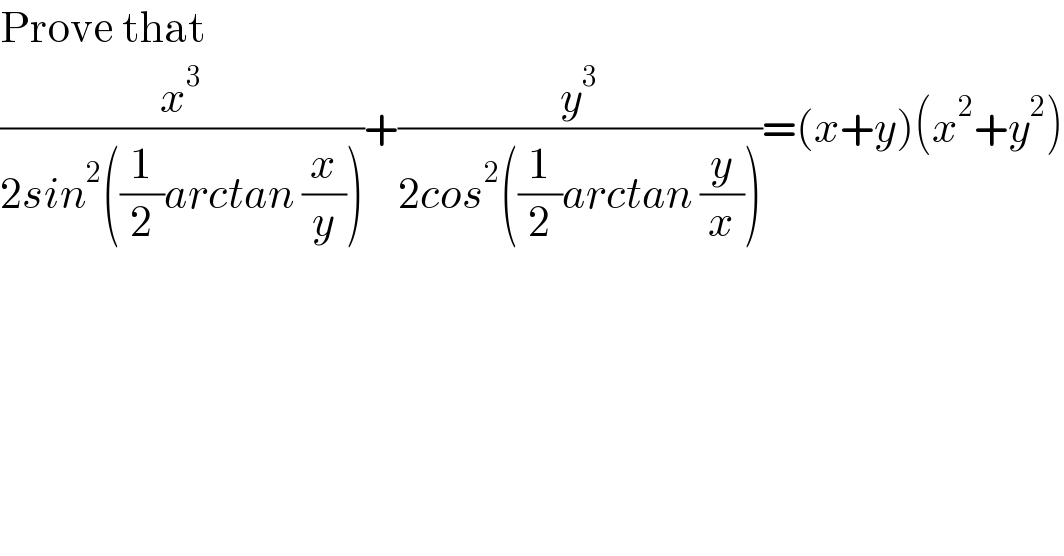
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\:\frac{{x}}{{y}}\right)}+\frac{{y}^{\mathrm{3}} }{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\:\frac{{y}}{{x}}\right)}=\left({x}+{y}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$
Answered by Frix last updated on 25/Jul/23
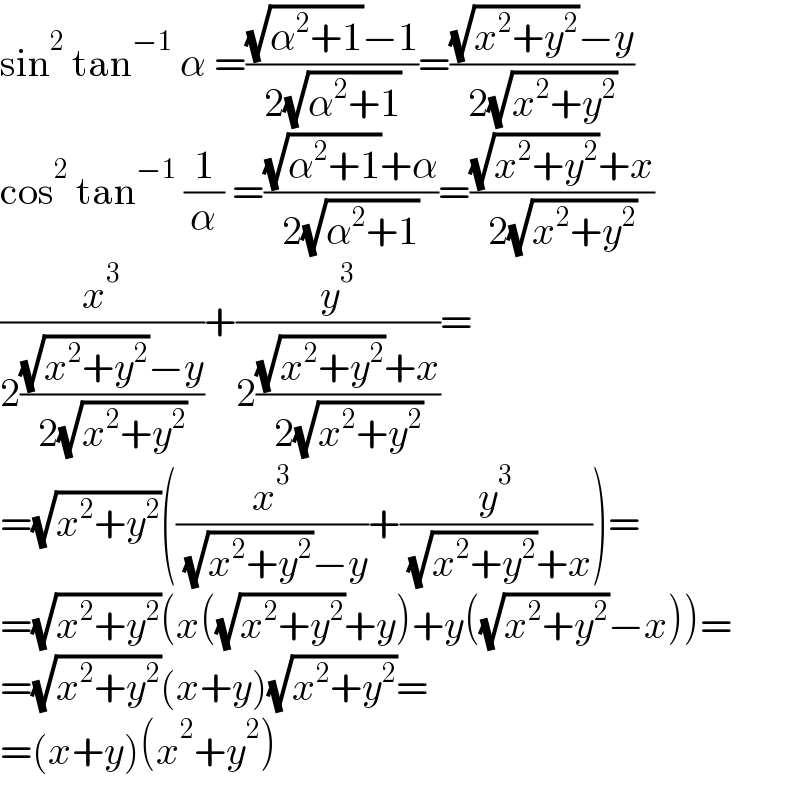
$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{tan}^{−\mathrm{1}} \:\alpha\:=\frac{\sqrt{\alpha^{\mathrm{2}} +\mathrm{1}}−\mathrm{1}}{\mathrm{2}\sqrt{\alpha^{\mathrm{2}} +\mathrm{1}}}=\frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }−{y}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\alpha}\:=\frac{\sqrt{\alpha^{\mathrm{2}} +\mathrm{1}}+\alpha}{\mathrm{2}\sqrt{\alpha^{\mathrm{2}} +\mathrm{1}}}=\frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+{x}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }} \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{2}\frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }−{y}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}}+\frac{{y}^{\mathrm{3}} }{\mathrm{2}\frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+{x}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}}= \\ $$$$=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\left(\frac{{x}^{\mathrm{3}} }{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }−{y}}+\frac{{y}^{\mathrm{3}} }{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+{x}}\right)= \\ $$$$=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\left({x}\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+{y}\right)+{y}\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }−{x}\right)\right)= \\ $$$$=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\left({x}+{y}\right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }= \\ $$$$=\left({x}+{y}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$
