
Question Number 158245 by HongKing last updated on 01/Nov/21
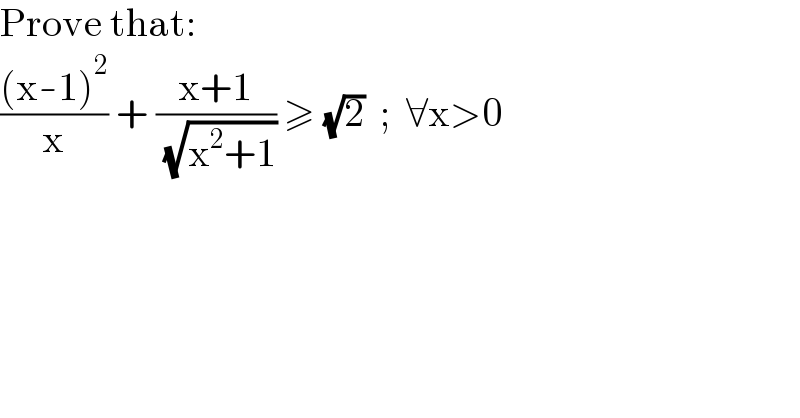
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\frac{\left(\mathrm{x}-\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}}\:+\:\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\:\geqslant\:\sqrt{\mathrm{2}}\:\:;\:\:\forall\mathrm{x}>\mathrm{0} \\ $$$$ \\ $$
Answered by mindispower last updated on 02/Nov/21
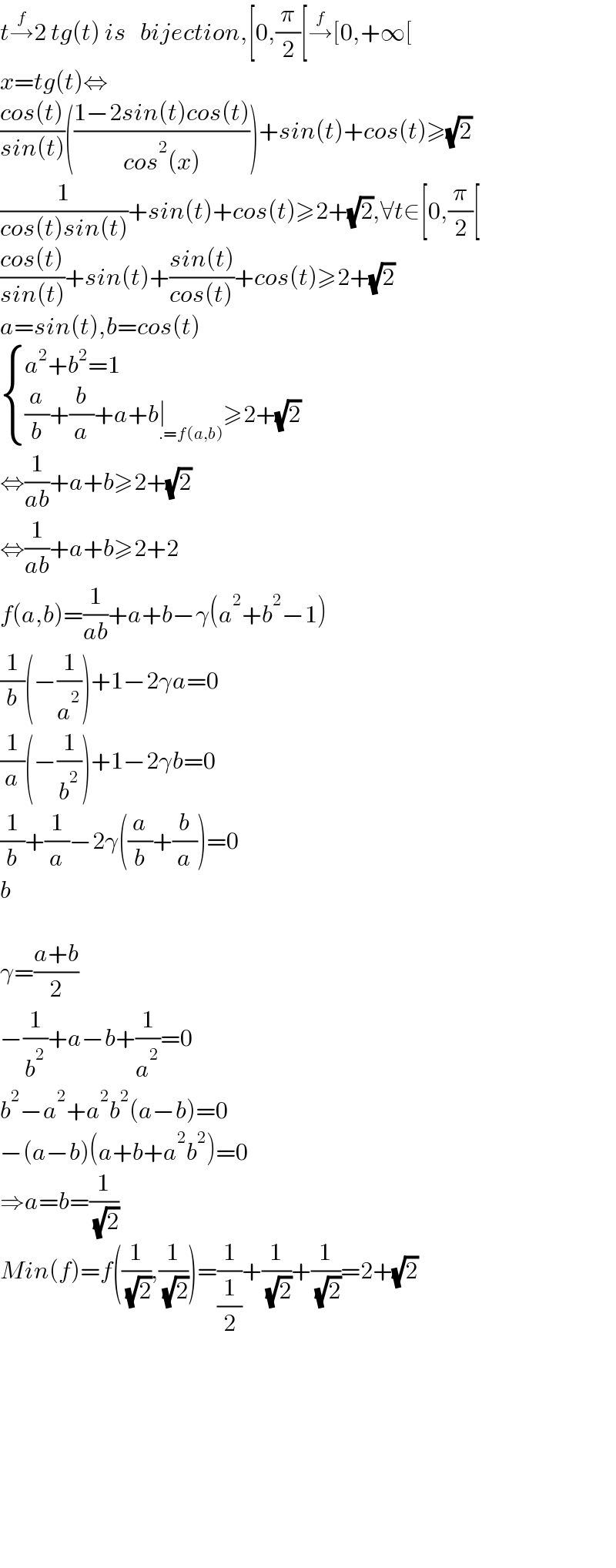
$${t}\overset{{f}} {\rightarrow}\mathrm{2}\:{tg}\left({t}\right)\:{is}\:\:\:{bijection},\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\overset{{f}} {\rightarrow}\left[\mathrm{0},+\infty\left[\right.\right.\right.\right. \\ $$$${x}={tg}\left({t}\right)\Leftrightarrow \\ $$$$\frac{{cos}\left({t}\right)}{{sin}\left({t}\right)}\left(\frac{\mathrm{1}−\mathrm{2}{sin}\left({t}\right){cos}\left({t}\right)}{{cos}^{\mathrm{2}} \left({x}\right)}\right)+{sin}\left({t}\right)+{cos}\left({t}\right)\geqslant\sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{cos}\left({t}\right){sin}\left({t}\right)}+{sin}\left({t}\right)+{cos}\left({t}\right)\geqslant\mathrm{2}+\sqrt{\mathrm{2}},\forall{t}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\right.\right. \\ $$$$\frac{{cos}\left({t}\right)}{{sin}\left({t}\right)}+{sin}\left({t}\right)+\frac{{sin}\left({t}\right)}{{cos}\left({t}\right)}+{cos}\left({t}\right)\geqslant\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$${a}={sin}\left({t}\right),{b}={cos}\left({t}\right) \\ $$$$\begin{cases}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1}}\\{\frac{{a}}{{b}}+\frac{{b}}{{a}}+{a}+{b}\underset{.={f}\left({a},{b}\right)} {\mid}\geqslant\mathrm{2}+\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{{ab}}+{a}+{b}\geqslant\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{{ab}}+{a}+{b}\geqslant\mathrm{2}+\mathrm{2} \\ $$$${f}\left({a},{b}\right)=\frac{\mathrm{1}}{{ab}}+{a}+{b}−\gamma\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{{b}}\left(−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)+\mathrm{1}−\mathrm{2}\gamma{a}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{a}}\left(−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)+\mathrm{1}−\mathrm{2}\gamma{b}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{a}}−\mathrm{2}\gamma\left(\frac{{a}}{{b}}+\frac{{b}}{{a}}\right)=\mathrm{0} \\ $$$${b} \\ $$$$ \\ $$$$\gamma=\frac{{a}+{b}}{\mathrm{2}} \\ $$$$−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+{a}−{b}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$${b}^{\mathrm{2}} −{a}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}−{b}\right)=\mathrm{0} \\ $$$$−\left({a}−{b}\right)\left({a}+{b}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{a}={b}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${Min}\left({f}\right)={f}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}},\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by HongKing last updated on 02/Nov/21
$$\mathrm{perfect}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser},\:\mathrm{thank}\:\mathrm{you} \\ $$
