
Question Number 37733 by kunal1234523 last updated on 17/Jun/18
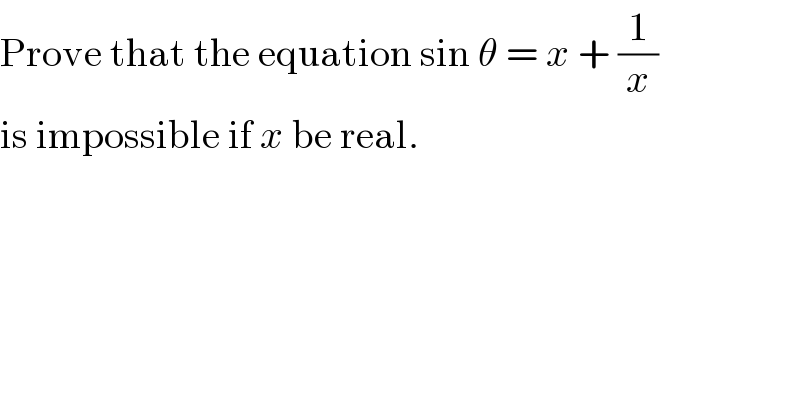
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{sin}\:\theta\:=\:{x}\:+\:\frac{\mathrm{1}}{{x}}\: \\ $$$$\mathrm{is}\:\mathrm{impossible}\:\mathrm{if}\:{x}\:\mathrm{be}\:\mathrm{real}. \\ $$
Answered by MrW3 last updated on 17/Jun/18
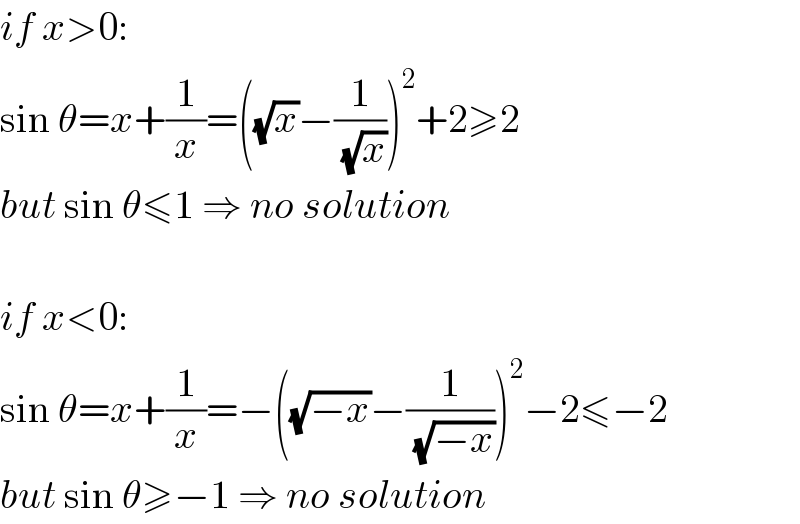
$${if}\:{x}>\mathrm{0}: \\ $$$$\mathrm{sin}\:\theta={x}+\frac{\mathrm{1}}{{x}}=\left(\sqrt{{x}}−\frac{\mathrm{1}}{\sqrt{{x}}}\right)^{\mathrm{2}} +\mathrm{2}\geqslant\mathrm{2} \\ $$$${but}\:\mathrm{sin}\:\theta\leqslant\mathrm{1}\:\Rightarrow\:{no}\:{solution} \\ $$$$ \\ $$$${if}\:{x}<\mathrm{0}: \\ $$$$\mathrm{sin}\:\theta={x}+\frac{\mathrm{1}}{{x}}=−\left(\sqrt{−{x}}−\frac{\mathrm{1}}{\sqrt{−{x}}}\right)^{\mathrm{2}} −\mathrm{2}\leqslant−\mathrm{2} \\ $$$${but}\:\mathrm{sin}\:\theta\geqslant−\mathrm{1}\:\Rightarrow\:{no}\:{solution} \\ $$
Commented by kunal1234523 last updated on 17/Jun/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{MrW3} \\ $$
