
Question Number 105456 by 1549442205PVT last updated on 29/Jul/20

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{y}=\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{2x} \\ $$$$\mathrm{does}\:\mathrm{not}\:\mathrm{meet}\:\mathrm{the}\:\mathrm{straight}\:\mathrm{line} \\ $$$$\mathrm{y}=\mathrm{2x}−\mathrm{1}\:\mathrm{and}\:\mathrm{find}\:\mathrm{the}\:\mathrm{distace}\:\mathrm{between} \\ $$$$\mathrm{their}\:\mathrm{nearest}\:\mathrm{points}.\left(\mathrm{Answer}\:\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\right) \\ $$
Answered by ajfour last updated on 29/Jul/20
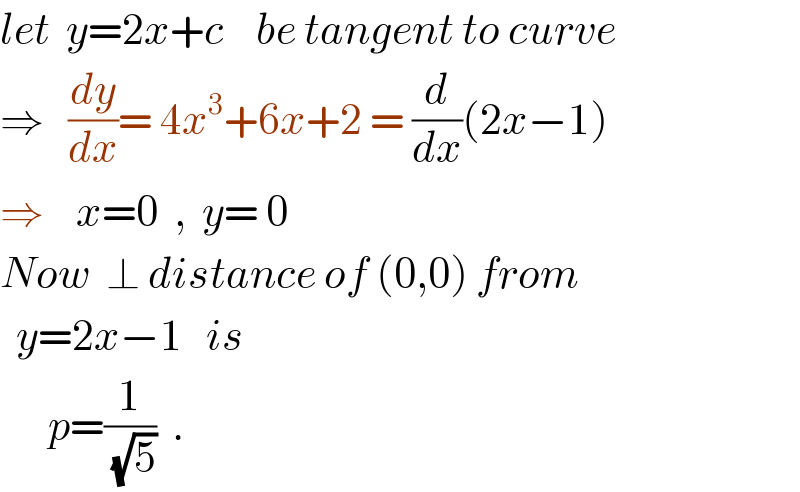
$${let}\:\:{y}=\mathrm{2}{x}+{c}\:\:\:\:{be}\:{tangent}\:{to}\:{curve} \\ $$$$\Rightarrow\:\:\:\frac{{dy}}{{dx}}=\:\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}+\mathrm{2}\:=\:\frac{{d}}{{dx}}\left(\mathrm{2}{x}−\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\:\:{x}=\mathrm{0}\:\:,\:\:{y}=\:\mathrm{0} \\ $$$${Now}\:\:\bot\:{distance}\:{of}\:\left(\mathrm{0},\mathrm{0}\right)\:{from} \\ $$$$\:\:{y}=\mathrm{2}{x}−\mathrm{1}\:\:\:{is} \\ $$$$\:\:\:\:\:\:{p}=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\:. \\ $$
Commented by Ari last updated on 29/Jul/20
Sir, if you can, clarify through actions your reasoning that there is ambiguity
Commented by 1549442205PVT last updated on 29/Jul/20
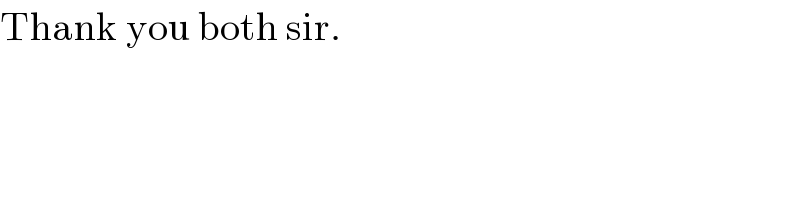
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{both}\:\mathrm{sir}. \\ $$
Answered by 1549442205PVT last updated on 29/Jul/20

$$\left.\mathrm{i}\right)\mathrm{Abscissa}\:\mathrm{of}\:\mathrm{intersection}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{4}\:} +\mathrm{3x}^{\mathrm{2}\:\:} +\mathrm{2x}\:\left(\mathrm{C}\right)\mathrm{and}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{2x}−\mathrm{1}\left(\mathrm{L}\right) \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{real}\:\mathrm{root}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{x}^{\mathrm{4}\:} +\mathrm{3x}^{\mathrm{2}\:\:} +\mathrm{2x}=\mathrm{2x}−\mathrm{1}\Leftrightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{But}\:\mathrm{this}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{roots} \\ $$$$\mathrm{simce}\:\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\geqslant\mathrm{1}\forall\mathrm{x}\in\mathbb{R}.\mathrm{Hence}\:\mathrm{the} \\ $$$$\mathrm{curve}\:\left(\mathrm{C}\right)\mathrm{don}'\mathrm{t}\:\mathrm{meet}\:\mathrm{the}\:\mathrm{line}\left(\mathrm{L}\right)\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{Denote}\:\mathrm{by}\:\mathrm{A}\left(\mathrm{x}_{\mathrm{0}} ,\mathrm{y}_{\mathrm{0}} \right)\mathrm{be}\:\mathrm{a}\:\mathrm{point}\:\mathrm{at} \\ $$$$\mathrm{which}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{parallel} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{2x}+\mathrm{1}\:.\mathrm{Then}\: \\ $$$$\left(\mathrm{x}^{\mathrm{4}\:} +\mathrm{3x}^{\mathrm{2}\:\:} +\mathrm{2x}\right)^{'} \mid_{\mathrm{x}_{\mathrm{0}} } =\mathrm{2}\Leftrightarrow\mathrm{4x}_{\mathrm{0}} ^{\mathrm{3}} +\mathrm{6x}_{\mathrm{0}} +\mathrm{2}=\mathrm{2} \\ $$$$\Leftrightarrow\mathrm{2x}_{\mathrm{0}} \left(\mathrm{2x}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{3}\right)=\mathrm{0}\Leftrightarrow\mathrm{x}_{\mathrm{0}} =\mathrm{0}\Rightarrow\mathrm{y}_{\mathrm{0}} =\mathrm{0}.\mathrm{Then}\: \\ $$$$\mathrm{the}\:\mathrm{nearest}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{line}\:\mathrm{be}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{A}\left(\mathrm{x}_{\mathrm{0}} ,\mathrm{y}_{\mathrm{0}} \right)\:\mathrm{and}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{2x}−\mathrm{1which} \\ $$$$\mathrm{means}\:\mathrm{d}_{\mathrm{0}} =\frac{\mid\mathrm{2}.\mathrm{0}−\mathrm{1}.\mathrm{0}\mid}{\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}} \\ $$
Commented by Ari last updated on 29/Jul/20
you are right
