
Question Number 119839 by ZiYangLee last updated on 27/Oct/20
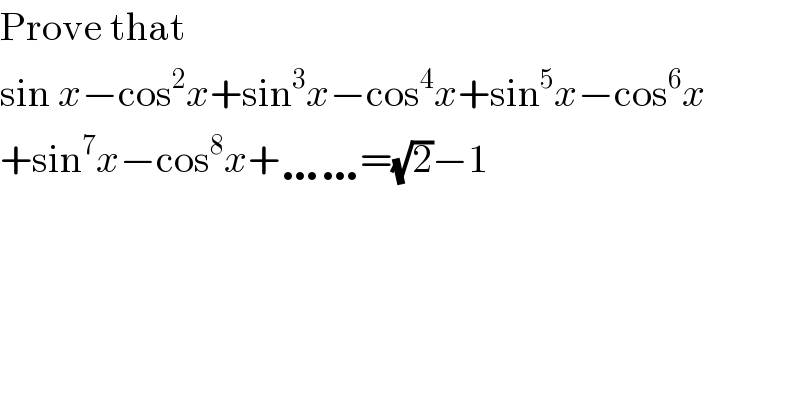
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{sin}\:{x}−\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{3}} {x}−\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{5}} {x}−\mathrm{cos}^{\mathrm{6}} {x} \\ $$$$+\mathrm{sin}^{\mathrm{7}} {x}−\mathrm{cos}^{\mathrm{8}} {x}+\ldots\ldots=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$
Answered by TANMAY PANACEA last updated on 27/Oct/20
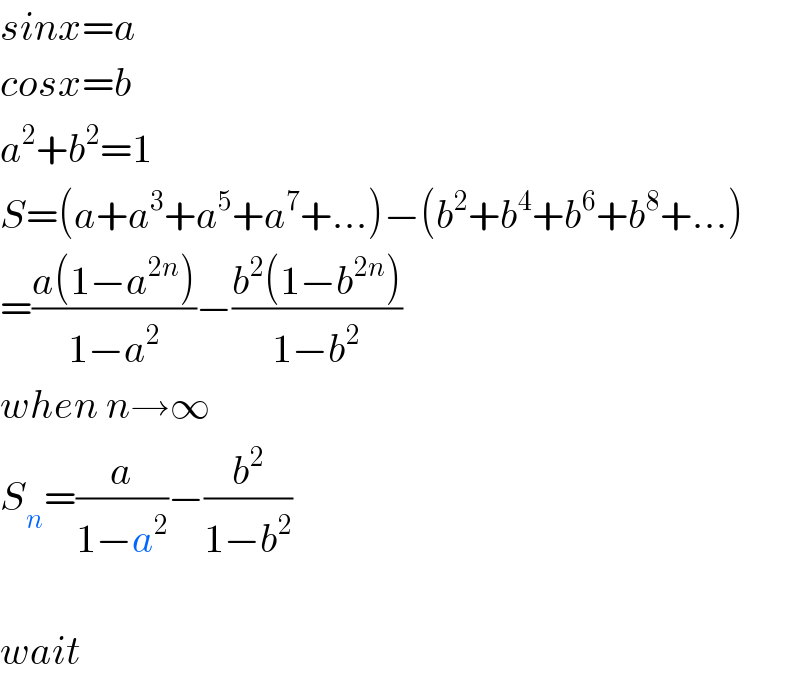
$${sinx}={a} \\ $$$${cosx}={b} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$${S}=\left({a}+{a}^{\mathrm{3}} +{a}^{\mathrm{5}} +{a}^{\mathrm{7}} +...\right)−\left({b}^{\mathrm{2}} +{b}^{\mathrm{4}} +{b}^{\mathrm{6}} +{b}^{\mathrm{8}} +...\right) \\ $$$$=\frac{{a}\left(\mathrm{1}−{a}^{\mathrm{2}{n}} \right)}{\mathrm{1}−{a}^{\mathrm{2}} }−\frac{{b}^{\mathrm{2}} \left(\mathrm{1}−{b}^{\mathrm{2}{n}} \right)}{\mathrm{1}−{b}^{\mathrm{2}} } \\ $$$${when}\:{n}\rightarrow\infty \\ $$$${S}_{{n}} =\frac{{a}}{\mathrm{1}−{a}^{\mathrm{2}} }−\frac{{b}^{\mathrm{2}} }{\mathrm{1}−{b}^{\mathrm{2}} }\: \\ $$$$ \\ $$$${wait} \\ $$
