
Question Number 116281 by aye48 last updated on 02/Oct/20

$$\mathrm{Prove}\:\mathrm{that}\:\:\:\mathrm{sin}\:\mathrm{10}°\:\mathrm{sin}\:\mathrm{30}°\:\mathrm{sin}\:\mathrm{50}°\:\mathrm{sin}\:\mathrm{70}°. \\ $$
Answered by Dwaipayan Shikari last updated on 02/Oct/20
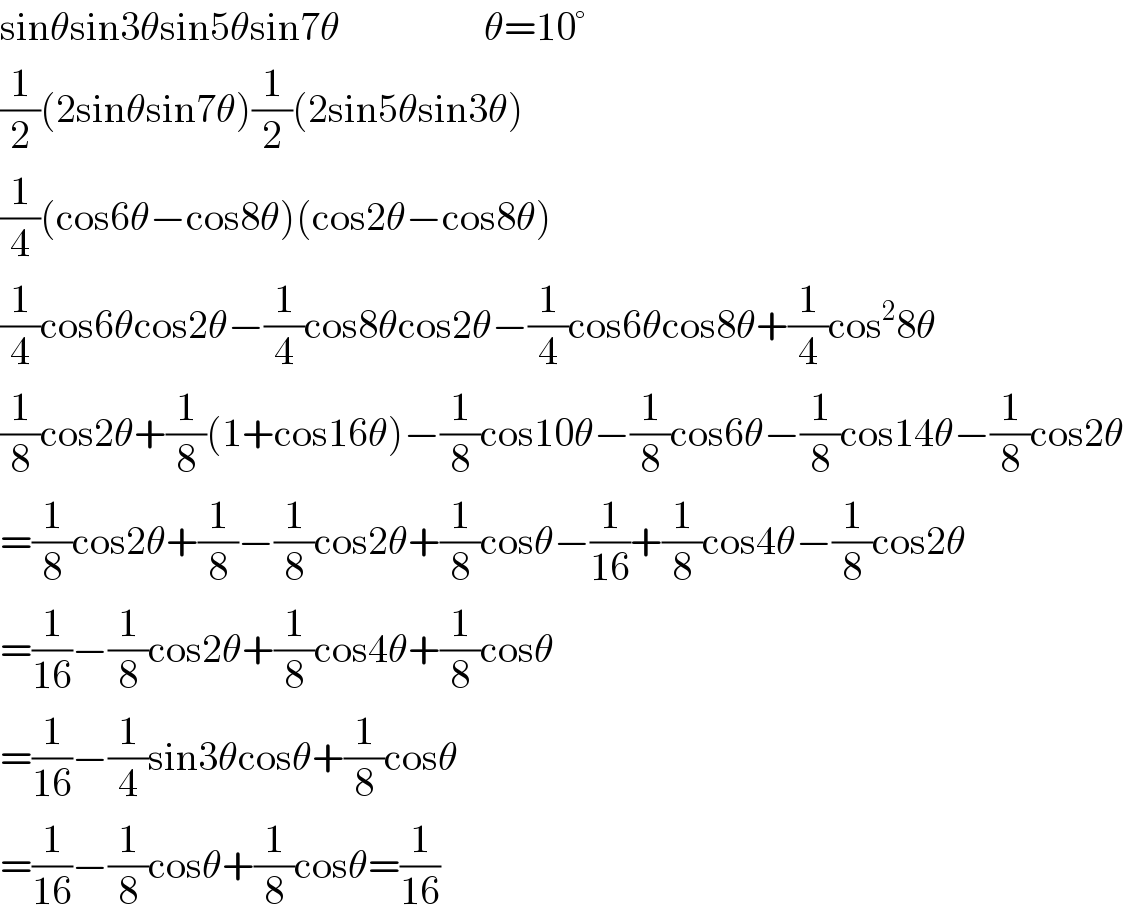
$$\mathrm{sin}\theta\mathrm{sin3}\theta\mathrm{sin5}\theta\mathrm{sin7}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta=\mathrm{10}° \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2sin}\theta\mathrm{sin7}\theta\right)\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2sin5}\theta\mathrm{sin3}\theta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{cos6}\theta−\mathrm{cos8}\theta\right)\left(\mathrm{cos2}\theta−\mathrm{cos8}\theta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos6}\theta\mathrm{cos2}\theta−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos8}\theta\mathrm{cos2}\theta−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos6}\theta\mathrm{cos8}\theta+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}^{\mathrm{2}} \mathrm{8}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos2}\theta+\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}+\mathrm{cos16}\theta\right)−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos10}\theta−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos6}\theta−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos14}\theta−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos2}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos2}\theta+\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos2}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\theta−\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos4}\theta−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos2}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos2}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos4}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin3}\theta\mathrm{cos}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\theta=\frac{\mathrm{1}}{\mathrm{16}} \\ $$
Answered by TANMAY PANACEA last updated on 02/Oct/20
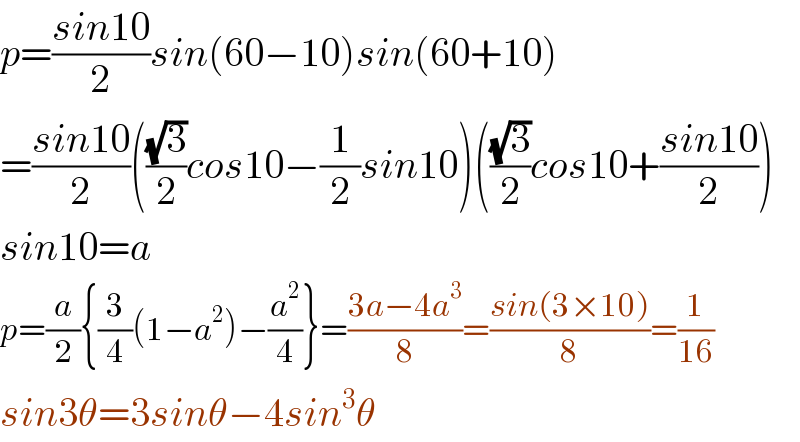
$${p}=\frac{{sin}\mathrm{10}}{\mathrm{2}}{sin}\left(\mathrm{60}−\mathrm{10}\right){sin}\left(\mathrm{60}+\mathrm{10}\right) \\ $$$$=\frac{{sin}\mathrm{10}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cos}\mathrm{10}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{10}\right)\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cos}\mathrm{10}+\frac{{sin}\mathrm{10}}{\mathrm{2}}\right) \\ $$$${sin}\mathrm{10}={a} \\ $$$${p}=\frac{{a}}{\mathrm{2}}\left\{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right\}=\frac{\mathrm{3}{a}−\mathrm{4}{a}^{\mathrm{3}} }{\mathrm{8}}=\frac{{sin}\left(\mathrm{3}×\mathrm{10}\right)}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${sin}\mathrm{3}\theta=\mathrm{3}{sin}\theta−\mathrm{4}{sin}^{\mathrm{3}} \theta \\ $$
