
Question Number 7621 by 314159 last updated on 06/Sep/16
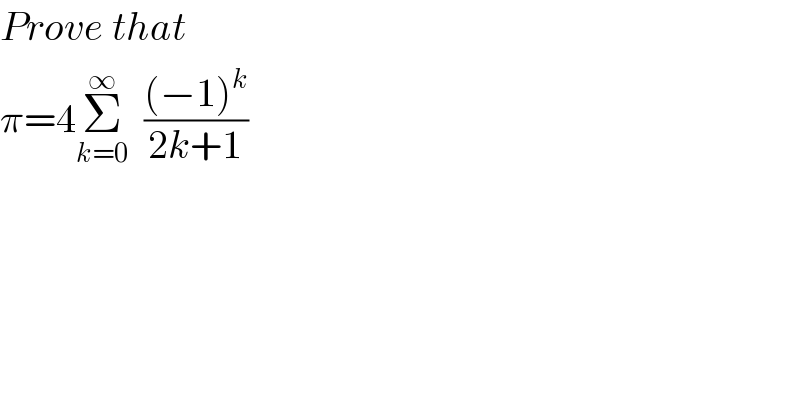
$${Prove}\:{that}\: \\ $$$$\pi=\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}} \\ $$
Answered by prakash jain last updated on 26/Sep/16
![Outline for the proof: x<1 (1/(1+x^2 ))=1−x^2 +x^4 −x^6 +x^8 −+.. Integrate from 0 to 1. ∫_0 ^1 (1/(1+x^2 ))=∫_0 ^1 1−x^2 +x^4 −x^6 [tan^(−1) x]_0 ^1 =[x−(x^3 /3)+(x^5 /5)−(x^7 /7)+−..]_0 ^1 (π/4)=1−(1/3)+(1/5)−(1/7)+−... (π/4)=Σ_(k=0) ^∞ (((−1)^k )/(2k+1))](Q7986.png)
$$\mathrm{Outline}\:\mathrm{for}\:\mathrm{the}\:\mathrm{proof}: \\ $$$${x}<\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −{x}^{\mathrm{6}} +{x}^{\mathrm{8}} −+.. \\ $$$$\mathrm{Integrate}\:\mathrm{from}\:\mathrm{0}\:\mathrm{to}\:\mathrm{1}. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −{x}^{\mathrm{6}} \\ $$$$\left[\mathrm{tan}^{−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} =\left[{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}}+−..\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\frac{\pi}{\mathrm{4}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+−... \\ $$$$\frac{\pi}{\mathrm{4}}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}} \\ $$
