
Question Number 188776 by depressiveshrek last updated on 06/Mar/23
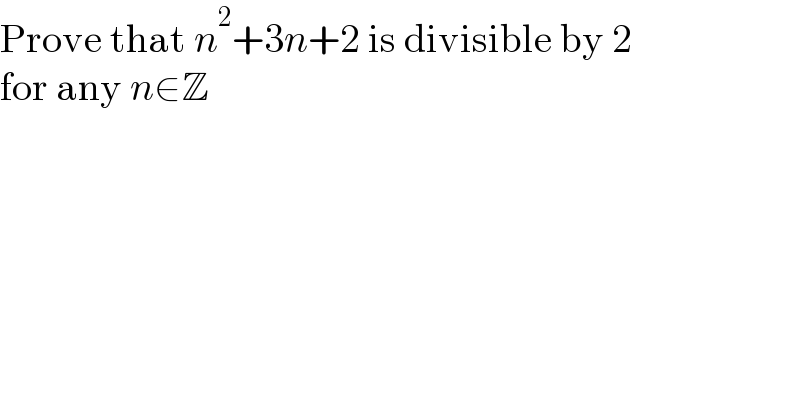
$$\mathrm{Prove}\:\mathrm{that}\:{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2} \\ $$$$\mathrm{for}\:\mathrm{any}\:{n}\in\mathbb{Z} \\ $$
Commented by Frix last updated on 08/Mar/23
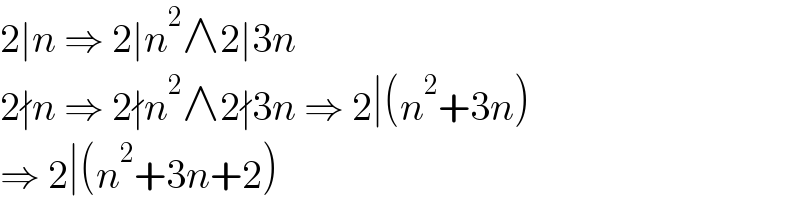
$$\mathrm{2}\mid{n}\:\Rightarrow\:\mathrm{2}\mid{n}^{\mathrm{2}} \wedge\mathrm{2}\mid\mathrm{3}{n} \\ $$$$\mathrm{2}\nmid{n}\:\Rightarrow\:\mathrm{2}\nmid{n}^{\mathrm{2}} \wedge\mathrm{2}\nmid\mathrm{3}{n}\:\Rightarrow\:\mathrm{2}\mid\left({n}^{\mathrm{2}} +\mathrm{3}{n}\right) \\ $$$$\Rightarrow\:\mathrm{2}\mid\left({n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}\right) \\ $$
Answered by witcher3 last updated on 06/Mar/23
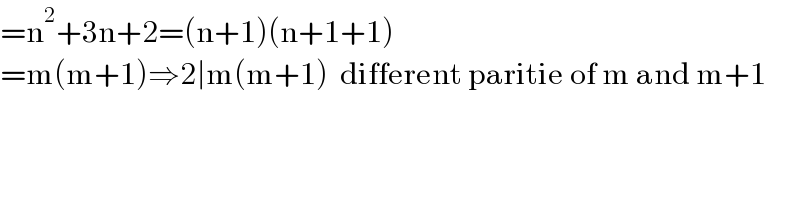
$$=\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{2}=\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{1}+\mathrm{1}\right) \\ $$$$=\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)\Rightarrow\mathrm{2}\mid\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)\:\:\mathrm{different}\:\mathrm{paritie}\:\mathrm{of}\:\mathrm{m}\:\mathrm{and}\:\mathrm{m}+\mathrm{1} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 06/Mar/23

mind is power 🔥
Commented by Rasheed.Sindhi last updated on 07/Mar/23

$$\left.'{mindispower}'\:{is}\:{registered}\:'{trade}'{mark}!\::\right) \\ $$
Commented by ARUNG_Brandon_MBU last updated on 07/Mar/23
��
Commented by witcher3 last updated on 07/Mar/23

$$\mathrm{yes}\:\mathrm{its}\:\mathrm{mee} \\ $$$$\mathrm{1}\:\mathrm{st}\:\mathrm{Broken}\:\mathrm{Phone} \\ $$$$\mathrm{2nd}\:\mathrm{stole}\:\mathrm{My}\:\mathrm{Phone} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Mar/23
$${Welcome}\:{sir}\:{mindispower}\:{with} \\ $$$${your}\:{new}\:{ID}. \\ $$
Commented by Rasheed.Sindhi last updated on 08/Mar/23
$$@\:{Ar}\:{Brandon} \\ $$$${How}\:{you}\:{guessed}\:{that}?\:{This}\:{time} \\ $$$${also}\:{correctly}\:!!! \\ $$
Commented by witcher3 last updated on 08/Mar/23

$$\mathrm{thank}\:\mathrm{You}\:\mathrm{Sir} \\ $$
Commented by witcher3 last updated on 08/Mar/23

$$\mathrm{sir}\:\mathrm{Arun}\:\mathrm{do}\:\mathrm{You}\:\mathrm{Know}\:\mathrm{if}\:\mathrm{Python}\:\mathrm{worcks} \\ $$$$\mathrm{in}\:\mathrm{IOS}\:\mathrm{10}.\mathrm{1} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 09/Mar/23
Here is what Chat GPT says: Yes, Python can work on iOS 10.1. However, this will require some additional steps, as Python does not come pre-installed on iOS devices. There are several ways to install Python on iOS, but the easiest method is to use a third-party app like Pythonista or Pyto, which allow you to write and run Python code directly on your iOS device. Once you have installed the Python app of your choice, you should be able to create and run Python scripts on your iOS device just like you would on a computer. However, it's worth noting that the version of Python available on iOS may be slightly different from the version you're used to running on your computer, and some libraries and modules may not be available. Also, it is important to understand that Python on iOS can be limited in terms of the operations that it can perform, especially when it comes to interacting with other apps or the system. This is due to the strict security protocols that Apple has in place to protect their devices.
Commented by ARUNG_Brandon_MBU last updated on 09/Mar/23

$$\mathrm{Hello},\:\mathrm{Sir}\:\mathrm{Rasheed}\:!\:\mathrm{I}\:\mathrm{just}\:\mathrm{noticed}\:\mathrm{similarities} \\ $$$$\mathrm{in}\:\mathrm{his}\:\mathrm{expressions}\:\mathrm{with}\:\mathrm{this}\:\mathrm{account}\:\mathrm{and} \\ $$$$\:\mathrm{the}\:\mathrm{ones}\:\mathrm{of}\:\mathrm{his}\:\mathrm{previous}\:\mathrm{account}.\:\mathrm{The}\:\mathrm{level}\:\mathrm{of} \\ $$$$\mathrm{Calculus}\:\mathrm{questions}\:\mathrm{he}\:\mathrm{solves}.\:\mathrm{And}\:\mathrm{since}\:\mathrm{this}\:\mathrm{is}\:\mathrm{my} \\ $$$$\mathrm{favorite}\:\mathrm{topic}\:\mathrm{it}'\mathrm{s}\:\mathrm{normal}\:\mathrm{that}\:\mathrm{I}\:\mathrm{remark}\:\mathrm{those} \\ $$$$\mathrm{who}\:\mathrm{solve}\:\mathrm{tough}\:\mathrm{questions}\:\mathrm{there}\:\mathrm{and}\:\mathrm{also}\:\mathrm{their} \\ $$$$\mathrm{styles}.\:\mathrm{I}\:\mathrm{also}\:\mathrm{noticed}\:\mathrm{some}\:\mathrm{very}\:\mathrm{slight}\:\mathrm{grammar}\:\mathrm{mistakes} \\ $$$$\mathrm{common}\:\mathrm{to}\:\mathrm{both}\:\mathrm{accounts}\:\mathrm{and}\:\mathrm{also}\:\mathrm{the}\:\mathrm{greetings} \\ $$$$\left(\mathrm{with}\:\mathrm{pleasure},\:\mathrm{have}\:\mathrm{a}\:\mathrm{nice}\:\mathrm{day},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 09/Mar/23

$$\mathcal{G}{ood}\:{observing}! \\ $$$$\mathcal{T}{hanks}\:{sir}! \\ $$
Commented by witcher3 last updated on 16/Mar/23

$$\mathrm{thank}\:\mathrm{You}\:\mathrm{sir} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 16/Mar/23
Je vous en prie !
Answered by mehdee42 last updated on 06/Mar/23
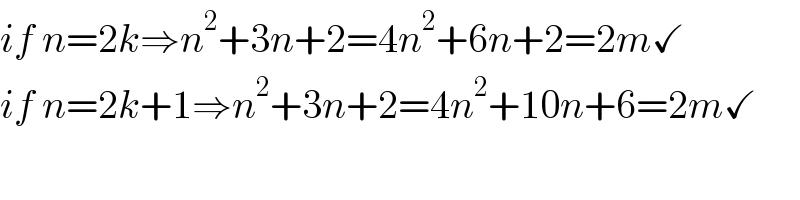
$${if}\:{n}=\mathrm{2}{k}\Rightarrow{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}=\mathrm{4}{n}^{\mathrm{2}} +\mathrm{6}{n}+\mathrm{2}=\mathrm{2}{m}\checkmark \\ $$$${if}\:{n}=\mathrm{2}{k}+\mathrm{1}\Rightarrow{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}=\mathrm{4}{n}^{\mathrm{2}} +\mathrm{10}{n}+\mathrm{6}=\mathrm{2}{m}\checkmark \\ $$$$ \\ $$
Answered by manxsol last updated on 06/Mar/23
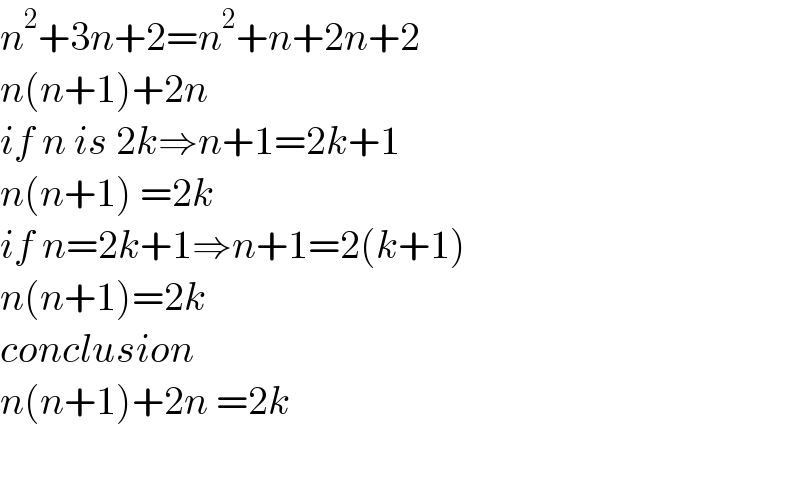
$${n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}={n}^{\mathrm{2}} +{n}+\mathrm{2}{n}+\mathrm{2} \\ $$$${n}\left({n}+\mathrm{1}\right)+\mathrm{2}{n} \\ $$$${if}\:{n}\:{is}\:\mathrm{2}{k}\Rightarrow{n}+\mathrm{1}=\mathrm{2}{k}+\mathrm{1} \\ $$$${n}\left({n}+\mathrm{1}\right)\:=\mathrm{2}{k} \\ $$$${if}\:{n}=\mathrm{2}{k}+\mathrm{1}\Rightarrow{n}+\mathrm{1}=\mathrm{2}\left({k}+\mathrm{1}\right) \\ $$$${n}\left({n}+\mathrm{1}\right)=\mathrm{2}{k} \\ $$$${conclusion} \\ $$$${n}\left({n}+\mathrm{1}\right)+\mathrm{2}{n}\:=\mathrm{2}{k} \\ $$$$ \\ $$
