
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 197311 by cortano12 last updated on 13/Sep/23
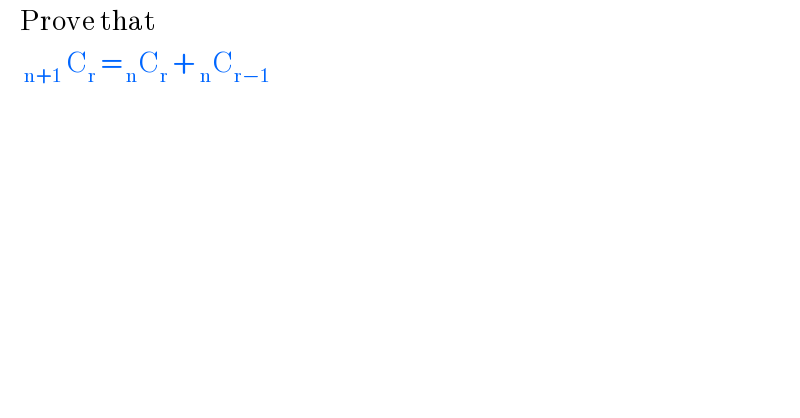
$$\:\:\:\:\:\mathrm{Prove}\:\mathrm{that}\: \\ $$$$\:\:\:\:\:\:_{\mathrm{n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{r}} \:=\:_{\mathrm{n}} \mathrm{C}_{\mathrm{r}} \:+\:_{\mathrm{n}} \mathrm{C}_{\mathrm{r}−\mathrm{1}} \: \\ $$
Answered by qaz last updated on 14/Sep/23
^(n+1) =[x^r ]((1+x)^n +x(1+x)^n ) = ((n),(r) )+ ((( n)),((r−1)) )](Q197353.png)
$$\begin{pmatrix}{{n}+\mathrm{1}}\\{\:\:\:{r}}\end{pmatrix}=\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{\:\:\:{n}}\\{{r}−\mathrm{1}}\end{pmatrix}\:\:? \\ $$$$\begin{pmatrix}{{n}+\mathrm{1}}\\{\:\:\:{r}}\end{pmatrix}=\left[{x}^{{r}} \right]\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} \\ $$$$=\left[{x}^{{r}} \right]\left(\left(\mathrm{1}+{x}\right)^{{n}} +{x}\left(\mathrm{1}+{x}\right)^{{n}} \right) \\ $$$$=\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{\:\:\:{n}}\\{{r}−\mathrm{1}}\end{pmatrix} \\ $$
