
Question Number 195708 by mokys last updated on 08/Aug/23
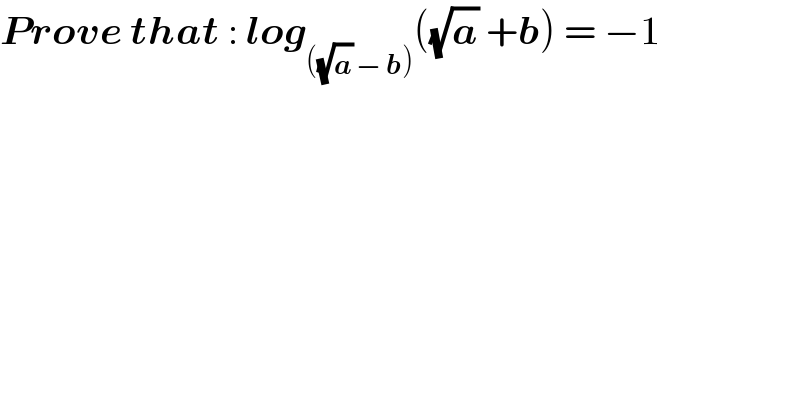
$$\boldsymbol{{Prove}}\:\boldsymbol{{that}}\::\:\boldsymbol{{log}}_{\left(\sqrt{\boldsymbol{{a}}}\:−\:\boldsymbol{{b}}\right)} \left(\sqrt{\boldsymbol{{a}}}\:+\boldsymbol{{b}}\right)\:=\:−\mathrm{1} \\ $$
Answered by JDamian last updated on 08/Aug/23
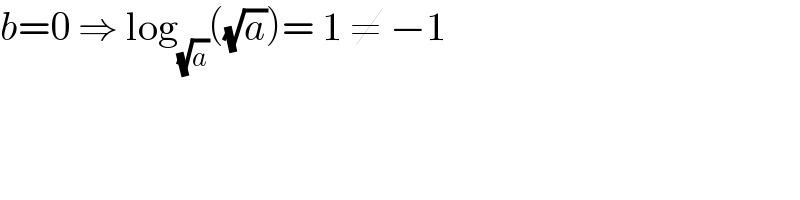
$${b}=\mathrm{0}\:\Rightarrow\:\mathrm{log}_{\sqrt{{a}}} \left(\sqrt{{a}}\right)=\:\mathrm{1}\:\neq\:−\mathrm{1} \\ $$
Answered by Frix last updated on 08/Aug/23
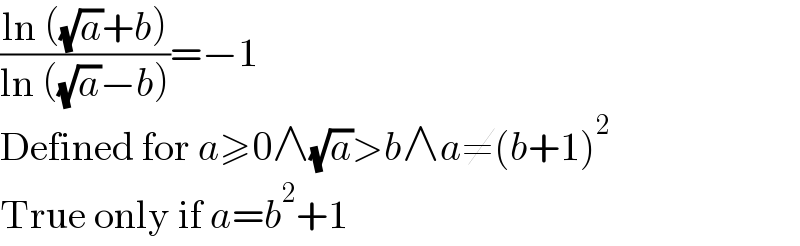
$$\frac{\mathrm{ln}\:\left(\sqrt{{a}}+{b}\right)}{\mathrm{ln}\:\left(\sqrt{{a}}−{b}\right)}=−\mathrm{1} \\ $$$$\mathrm{Defined}\:\mathrm{for}\:{a}\geqslant\mathrm{0}\wedge\sqrt{{a}}>{b}\wedge{a}\neq\left({b}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{True}\:\mathrm{only}\:\mathrm{if}\:{a}={b}^{\mathrm{2}} +\mathrm{1} \\ $$
