Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 77127 by peter frank last updated on 03/Jan/20

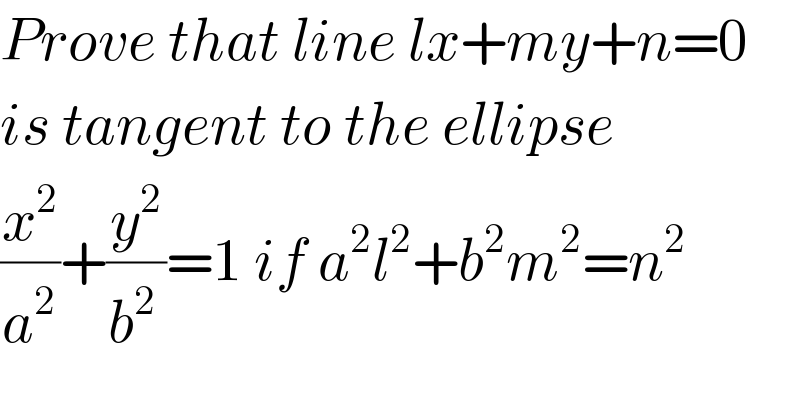
Prove that line lx+my+n=0 is tangent to the ellipse (x^2 /a^2 )+(y^2 /b^(2 ) )=1 if a^2 l^2 +b^2 m^2 =n^2

$${Prove}\:{that}\:{line}\:{lx}+{my}+{n}=\mathrm{0} \\ $$$${is}\:{tangent}\:{to}\:{the}\:{ellipse} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}\:} }=\mathrm{1}\:{if}\:{a}^{\mathrm{2}} {l}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} ={n}^{\mathrm{2}} \\ $$

Answered by jagoll last updated on 03/Jan/20

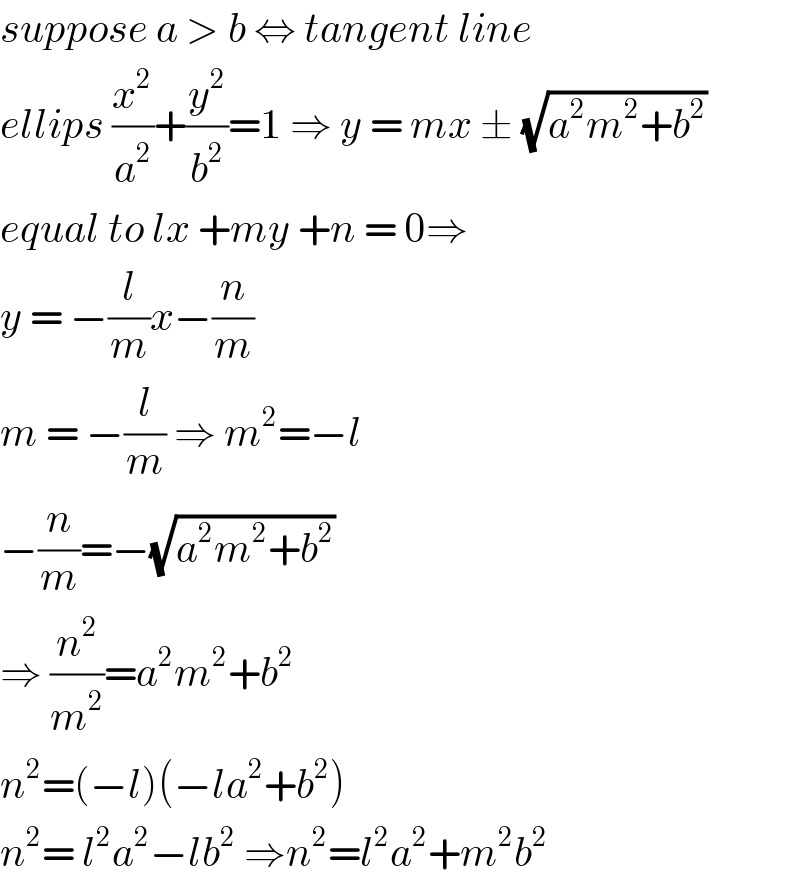
suppose a > b ⇔ tangent line ellips (x^2 /a^2 )+(y^2 /b^2 )=1 ⇒ y = mx ± (√(a^2 m^2 +b^2 )) equal to lx +my +n = 0⇒ y = −(l/m)x−(n/m) m = −(l/m) ⇒ m^2 =−l −(n/m)=−(√(a^2 m^2 +b^2 )) ⇒ (n^2 /m^2 )=a^2 m^2 +b^2 n^2 =(−l)(−la^2 +b^2 ) n^2 = l^2 a^2 −lb^2 ⇒n^2 =l^2 a^2 +m^2 b^2

$${suppose}\:{a}\:>\:{b}\:\Leftrightarrow\:{tangent}\:{line}\: \\ $$$${ellips}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\Rightarrow\:{y}\:=\:{mx}\:\pm\:\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${equal}\:{to}\:{lx}\:+{my}\:+{n}\:=\:\mathrm{0}\Rightarrow\: \\ $$$${y}\:=\:−\frac{{l}}{{m}}{x}−\frac{{n}}{{m}}\: \\ $$$${m}\:=\:−\frac{{l}}{{m}}\:\Rightarrow\:{m}^{\mathrm{2}} =−{l}\: \\ $$$$−\frac{{n}}{{m}}=−\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{{n}^{\mathrm{2}} }{{m}^{\mathrm{2}} }={a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} \: \\ $$$${n}^{\mathrm{2}} =\left(−{l}\right)\left(−{la}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\: \\ $$$${n}^{\mathrm{2}} =\:{l}^{\mathrm{2}} {a}^{\mathrm{2}} −{lb}^{\mathrm{2}} \:\Rightarrow{n}^{\mathrm{2}} ={l}^{\mathrm{2}} {a}^{\mathrm{2}} +{m}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$

Commented by peter frank last updated on 03/Jan/20

thank you

$${thank}\:{you} \\ $$

Answered by mr W last updated on 03/Jan/20

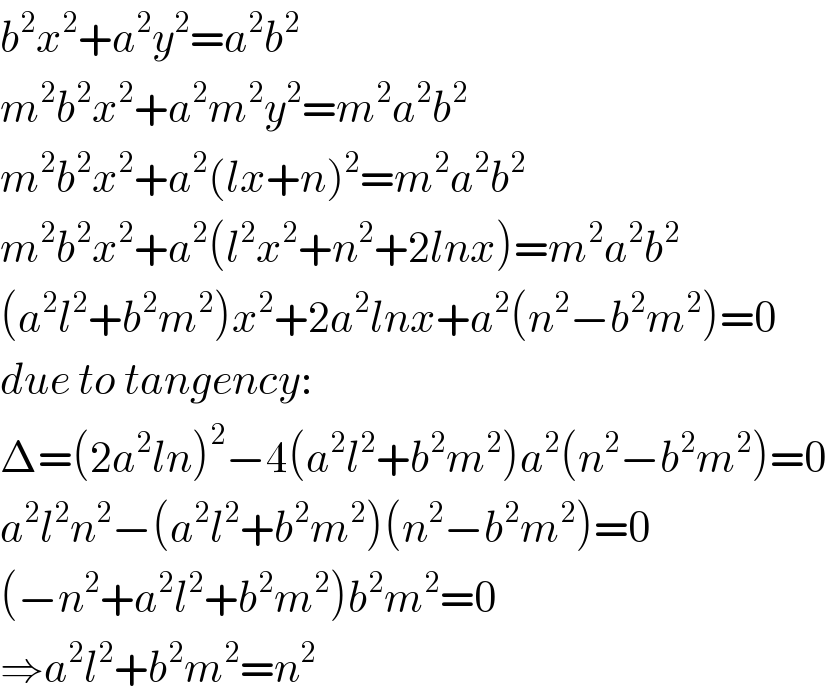
b^2 x^2 +a^2 y^2 =a^2 b^2 m^2 b^2 x^2 +a^2 m^2 y^2 =m^2 a^2 b^2 m^2 b^2 x^2 +a^2 (lx+n)^2 =m^2 a^2 b^2 m^2 b^2 x^2 +a^2 (l^2 x^2 +n^2 +2lnx)=m^2 a^2 b^2 (a^2 l^2 +b^2 m^2 )x^2 +2a^2 lnx+a^2 (n^2 −b^2 m^2 )=0 due to tangency: Δ=(2a^2 ln)^2 −4(a^2 l^2 +b^2 m^2 )a^2 (n^2 −b^2 m^2 )=0 a^2 l^2 n^2 −(a^2 l^2 +b^2 m^2 )(n^2 −b^2 m^2 )=0 (−n^2 +a^2 l^2 +b^2 m^2 )b^2 m^2 =0 ⇒a^2 l^2 +b^2 m^2 =n^2

$${b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${m}^{\mathrm{2}} {b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {m}^{\mathrm{2}} {y}^{\mathrm{2}} ={m}^{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${m}^{\mathrm{2}} {b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({lx}+{n}\right)^{\mathrm{2}} ={m}^{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${m}^{\mathrm{2}} {b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({l}^{\mathrm{2}} {x}^{\mathrm{2}} +{n}^{\mathrm{2}} +\mathrm{2}{lnx}\right)={m}^{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} {l}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {lnx}+{a}^{\mathrm{2}} \left({n}^{\mathrm{2}} −{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${due}\:{to}\:{tangency}: \\ $$$$\Delta=\left(\mathrm{2}{a}^{\mathrm{2}} {ln}\right)^{\mathrm{2}} −\mathrm{4}\left({a}^{\mathrm{2}} {l}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right){a}^{\mathrm{2}} \left({n}^{\mathrm{2}} −{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${a}^{\mathrm{2}} {l}^{\mathrm{2}} {n}^{\mathrm{2}} −\left({a}^{\mathrm{2}} {l}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right)\left({n}^{\mathrm{2}} −{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(−{n}^{\mathrm{2}} +{a}^{\mathrm{2}} {l}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right){b}^{\mathrm{2}} {m}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {l}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} ={n}^{\mathrm{2}} \\ $$

Commented by peter frank last updated on 03/Jan/20

thank you

$${thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com