Question and Answers Forum

All Questions      Topic List

Logic Questions

Previous in All Question      Next in All Question      

Previous in Logic      Next in Logic      

Question Number 196986 by Erico last updated on 05/Sep/23

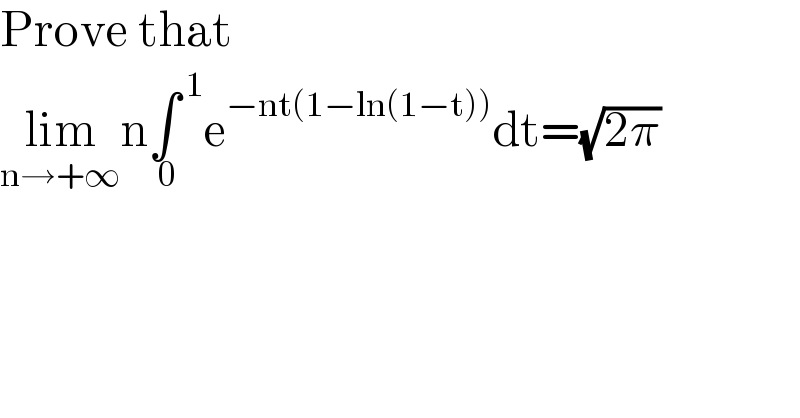
Prove that lim_(n→+∞) n∫^( 1) _( 0) e^(−nt(1−ln(1−t))) dt=(√(2π))

$$\mathrm{Prove}\:\mathrm{that}\: \\ $$$$\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}n}\underset{\:\mathrm{0}} {\int}^{\:\mathrm{1}} \mathrm{e}^{−\mathrm{nt}\left(\mathrm{1}−\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)\right)} \mathrm{dt}=\sqrt{\mathrm{2}\pi} \\ $$

Answered by witcher3 last updated on 07/Sep/23

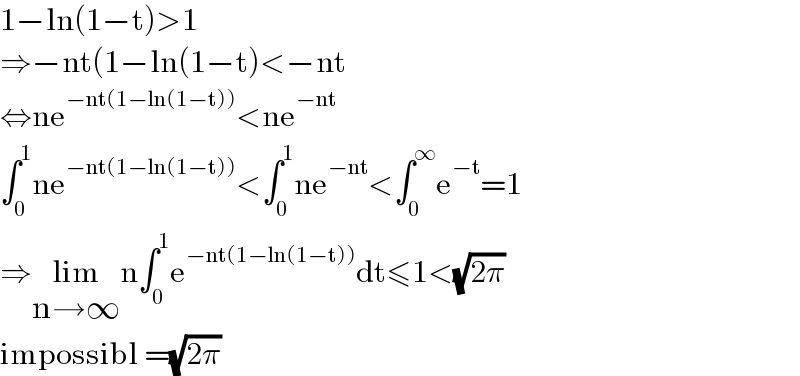
1−ln(1−t)>1 ⇒−nt(1−ln(1−t)<−nt ⇔ne^(−nt(1−ln(1−t))) <ne^(−nt) ∫_0 ^1 ne^(−nt(1−ln(1−t))) <∫_0 ^1 ne^(−nt) <∫_0 ^∞ e^(−t) =1 ⇒lim_(n→∞) n∫_0 ^1 e^(−nt(1−ln(1−t))) dt≤1<(√(2π)) impossibl =(√(2π))

$$\mathrm{1}−\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)>\mathrm{1} \\ $$$$\Rightarrow−\mathrm{nt}\left(\mathrm{1}−\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)<−\mathrm{nt}\right. \\ $$$$\Leftrightarrow\mathrm{ne}^{−\mathrm{nt}\left(\mathrm{1}−\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)\right)} <\mathrm{ne}^{−\mathrm{nt}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ne}^{−\mathrm{nt}\left(\mathrm{1}−\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)\right)} <\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ne}^{−\mathrm{nt}} <\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}} =\mathrm{1} \\ $$$$\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{−\mathrm{nt}\left(\mathrm{1}−\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)\right)} \mathrm{dt}\leqslant\mathrm{1}<\sqrt{\mathrm{2}\pi} \\ $$$$\mathrm{impossibl}\:=\sqrt{\mathrm{2}\pi} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com