
Question Number 210566 by Erico last updated on 12/Aug/24
![Prove that: if (x∈]−(π/2),(π/2)[ y =∫^( x) _( 0) (dt/(cos(t))) ) ⇒ (y∈IR x =∫^( y) _( 0) (dt/(cosh(t))) )](Q210566.png)
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\mathrm{if}\:\left(\mathrm{x}\in\right]−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\left[\:\:\mathrm{y}\:=\underset{\:\mathrm{0}} {\int}^{\:\mathrm{x}} \frac{\mathrm{dt}}{\mathrm{cos}\left(\mathrm{t}\right)}\:\right)\:\Rightarrow\:\:\left(\mathrm{y}\in\mathrm{IR}\:\:\:\mathrm{x}\:=\underset{\:\mathrm{0}} {\int}^{\:\mathrm{y}} \frac{\mathrm{dt}}{\mathrm{cosh}\left(\mathrm{t}\right)}\:\right) \\ $$
Answered by MrGaster last updated on 03/Feb/25
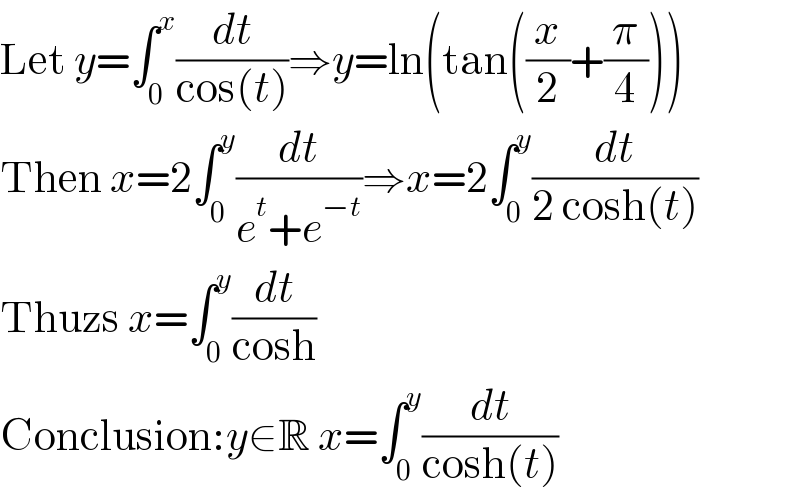
$$\mathrm{Let}\:{y}=\int_{\mathrm{0}} ^{{x}} \frac{{dt}}{\mathrm{cos}\left({t}\right)}\Rightarrow{y}=\mathrm{ln}\left(\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\right) \\ $$$$\mathrm{Then}\:{x}=\mathrm{2}\int_{\mathrm{0}} ^{{y}} \frac{{dt}}{{e}^{{t}} +{e}^{−{t}} }\Rightarrow{x}=\mathrm{2}\int_{\mathrm{0}} ^{{y}} \frac{{dt}}{\mathrm{2}\:\mathrm{cosh}\left({t}\right)} \\ $$$$\mathrm{Thuzs}\:{x}=\int_{\mathrm{0}} ^{{y}} \frac{{dt}}{\mathrm{cosh}} \\ $$$$\mathrm{Conclusion}:{y}\in\mathbb{R}\:{x}=\int_{\mathrm{0}} ^{{y}} \frac{{dt}}{\mathrm{cosh}\left({t}\right)} \\ $$
