
Question Number 98924 by Rio Michael last updated on 17/Jun/20
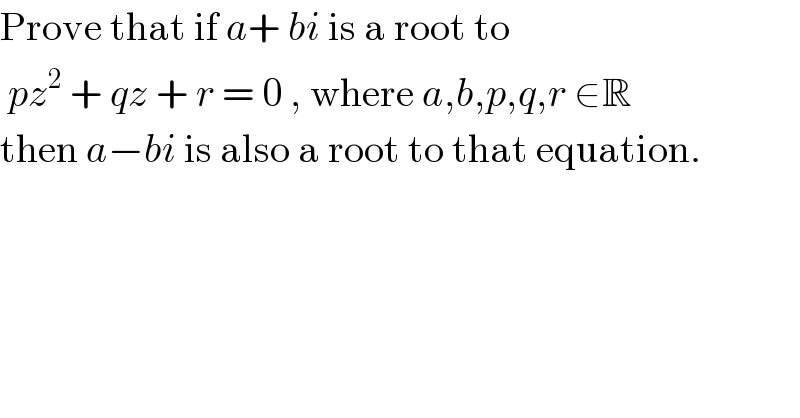
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{if}\:{a}+\:{bi}\:\mathrm{is}\:\mathrm{a}\:\mathrm{root}\:\mathrm{to} \\ $$$$\:{pz}^{\mathrm{2}} \:+\:{qz}\:+\:{r}\:=\:\mathrm{0}\:,\:\mathrm{where}\:{a},{b},{p},{q},{r}\:\in\mathbb{R} \\ $$$$\mathrm{then}\:{a}−{bi}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{root}\:\mathrm{to}\:\mathrm{that}\:\mathrm{equation}. \\ $$
