
Question Number 2751 by prakash jain last updated on 26/Nov/15
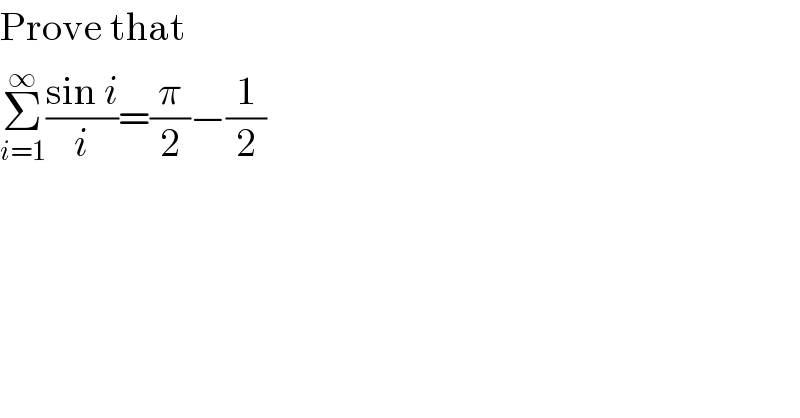
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\:{i}}{{i}}=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by prakash jain last updated on 27/Nov/15
![See question 2735 fo convergence proof. Question used i as index using n as index as i=(√(−1)) is used in answer. Σ_(n=1) ^∞ ((sin n)/n) =ℑ[Σ_(n=1) ^∞ (e^(in) /n)]=ℑ(ln (1−e^i ))=arg(1−e^i )=((π−1)/2)](Q2813.png)
$$\mathrm{See}\:\mathrm{question}\:\mathrm{2735}\:\mathrm{fo}\:\mathrm{convergence}\:\mathrm{proof}. \\ $$$$\mathrm{Question}\:\mathrm{used}\:{i}\:{as}\:{index}\:{using}\:{n}\:{as}\:{index}\: \\ $$$${as}\:{i}=\sqrt{−\mathrm{1}}\:{is}\:{used}\:{in}\:{answer}. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\:{n}}{{n}} \\ $$$$=\Im\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{in}} }{{n}}\right]=\Im\left(\mathrm{ln}\:\left(\mathrm{1}−{e}^{{i}} \right)\right)=\mathrm{arg}\left(\mathrm{1}−{e}^{{i}} \right)=\frac{\pi−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by prakash jain last updated on 27/Nov/15

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\:{nx}}{{n}}=\frac{\pi−{x}}{\mathrm{2}} \\ $$
