
Question Number 184062 by CrispyXYZ last updated on 02/Jan/23
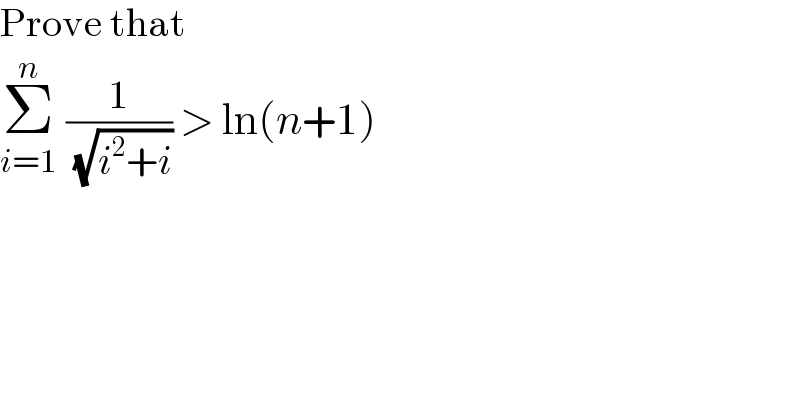
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{\:\sqrt{{i}^{\mathrm{2}} +{i}}}\:>\:\mathrm{ln}\left({n}+\mathrm{1}\right) \\ $$
Answered by mr W last updated on 02/Jan/23

$${things}\:{to}\:{know}: \\ $$$$\left.\mathrm{1}\right) \\ $$$$\frac{{a}+{b}}{\mathrm{2}}\geqslant\sqrt{{ab}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{ab}}}\geqslant\frac{\mathrm{2}}{{a}+{b}} \\ $$$$\left.\mathrm{2}\right) \\ $$$${f}\left({x}\right)=\mathrm{2}\left(\sqrt{{x}+\mathrm{1}}−\mathrm{1}\right)−\mathrm{ln}\:\left({x}+\mathrm{1}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{{x}+\mathrm{1}}}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{{x}+\mathrm{1}}}\right)>\mathrm{0} \\ $$$${it}\:{means}\:{for}\:{x}\geqslant\mathrm{0}\:{f}\left({x}\right)\:{is}\:{strictly} \\ $$$${increasing},{i}.{e}.\:{f}\left({x}\right)>\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left(\sqrt{{x}+\mathrm{1}}−\mathrm{1}\right)>\mathrm{ln}\:\left({x}+\mathrm{1}\right) \\ $$$$ \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}^{\mathrm{2}} +{i}}} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}\left({i}+\mathrm{1}\right)}} \\ $$$$\left.>\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{2}}{\:\sqrt{{i}}+\sqrt{{i}+\mathrm{1}}}\right)\:\:\:\:\:\:\:\:{see}\:\mathrm{1}\right)\:{above} \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\sqrt{{i}+\mathrm{1}}−\sqrt{{i}}\right) \\ $$$$=\mathrm{2}\left(\sqrt{{n}+\mathrm{1}}−\mathrm{1}\right) \\ $$$$\left.>\mathrm{ln}\:\left({n}+\mathrm{1}\right)\:\checkmark\:\:\:\:\:\:\:\:\:\:\:\:\:\:{see}\:\mathrm{2}\right)\:{above} \\ $$
