
Question Number 196412 by Erico last updated on 24/Aug/23
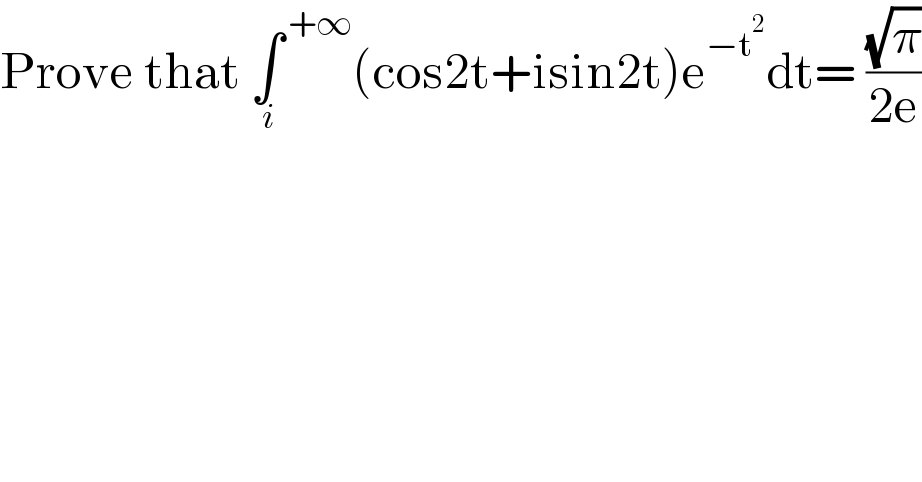
$$\mathrm{Prove}\:\mathrm{that}\:\underset{\:\mathrm{0}} {\int}^{\:{i}} \left({cos}\left(\mathrm{2}{t}\right)+{isin}\left(\mathrm{2}{t}\right)\right){e}^{−{t}^{\mathrm{2}} } {dt}=\:\frac{{i}}{\mathrm{2}{e}}\underset{\:\mathrm{0}} {\int}^{\:\mathrm{2}} \mathrm{e}^{\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}} \mathrm{dt} \\ $$
Commented by JDamian last updated on 24/Aug/23
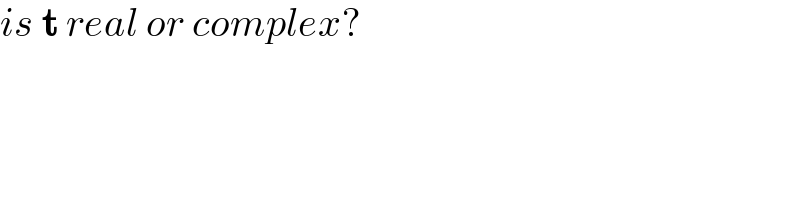
$${is}\:\boldsymbol{\mathrm{t}}\:{real}\:{or}\:{complex}? \\ $$
