
Question Number 8105 by 314159 last updated on 30/Sep/16
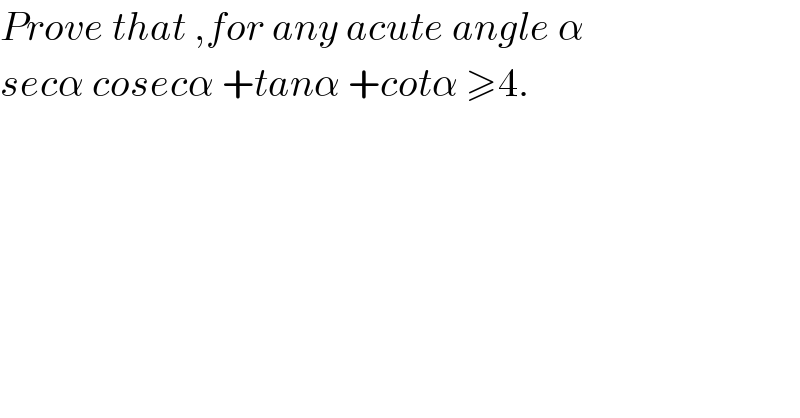
$${Prove}\:{that}\:,{for}\:{any}\:{acute}\:{angle}\:\alpha\: \\ $$$${sec}\alpha\:{cosec}\alpha\:+{tan}\alpha\:+{cot}\alpha\:\geqslant\mathrm{4}. \\ $$
Commented by Yozzia last updated on 30/Sep/16
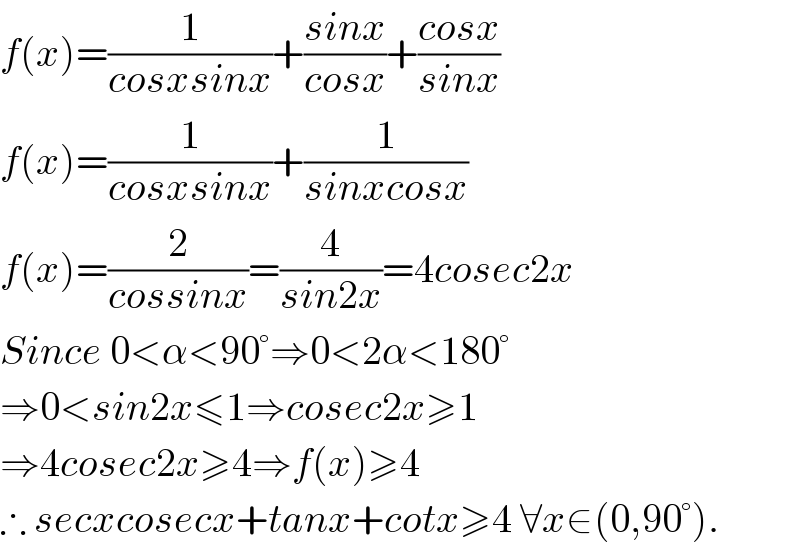
$${f}\left({x}\right)=\frac{\mathrm{1}}{{cosxsinx}}+\frac{{sinx}}{{cosx}}+\frac{{cosx}}{{sinx}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{cosxsinx}}+\frac{\mathrm{1}}{{sinxcosx}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}}{{cossinx}}=\frac{\mathrm{4}}{{sin}\mathrm{2}{x}}=\mathrm{4}{cosec}\mathrm{2}{x} \\ $$$${Since}\:\mathrm{0}<\alpha<\mathrm{90}°\Rightarrow\mathrm{0}<\mathrm{2}\alpha<\mathrm{180}° \\ $$$$\Rightarrow\mathrm{0}<{sin}\mathrm{2}{x}\leqslant\mathrm{1}\Rightarrow{cosec}\mathrm{2}{x}\geqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{4}{cosec}\mathrm{2}{x}\geqslant\mathrm{4}\Rightarrow{f}\left({x}\right)\geqslant\mathrm{4} \\ $$$$\therefore\:{secxcosecx}+{tanx}+{cotx}\geqslant\mathrm{4}\:\forall{x}\in\left(\mathrm{0},\mathrm{90}°\right). \\ $$
Answered by prakash jain last updated on 02/Oct/16

$$\mathrm{answer}\:\mathrm{in}\:\mathrm{coments} \\ $$
