
Previous in Relation and Functions Next in Relation and Functions
Question Number 10095 by Tawakalitu ayo mi last updated on 23/Jan/17
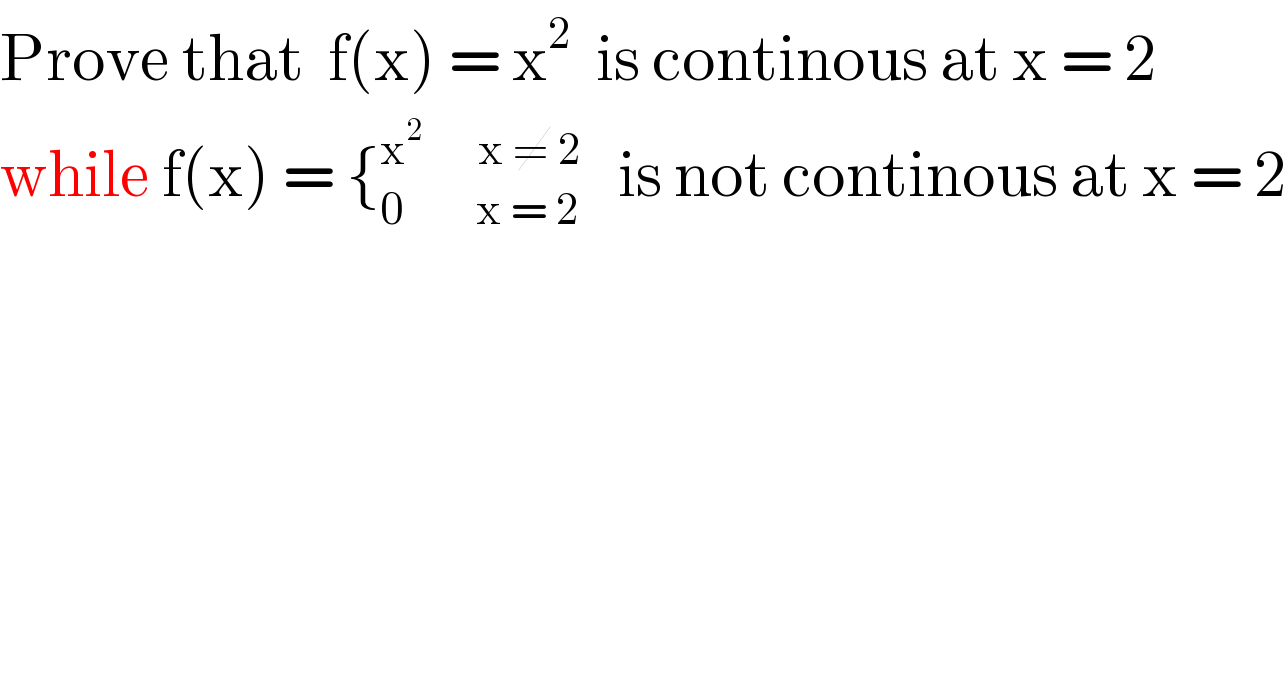
$$\mathrm{Prove}\:\mathrm{that}\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{2}} \:\:\mathrm{is}\:\mathrm{continous}\:\mathrm{at}\:\mathrm{x}\:=\:\mathrm{2} \\ $$$$\mathrm{while}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\left\{_{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{2}} ^{\mathrm{x}^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{x}\:\neq\:\mathrm{2}} \:\:\:\mathrm{is}\:\mathrm{not}\:\mathrm{continous}\:\mathrm{at}\:\mathrm{x}\:=\:\mathrm{2}\right. \\ $$
Answered by sandy_suhendra last updated on 23/Jan/17
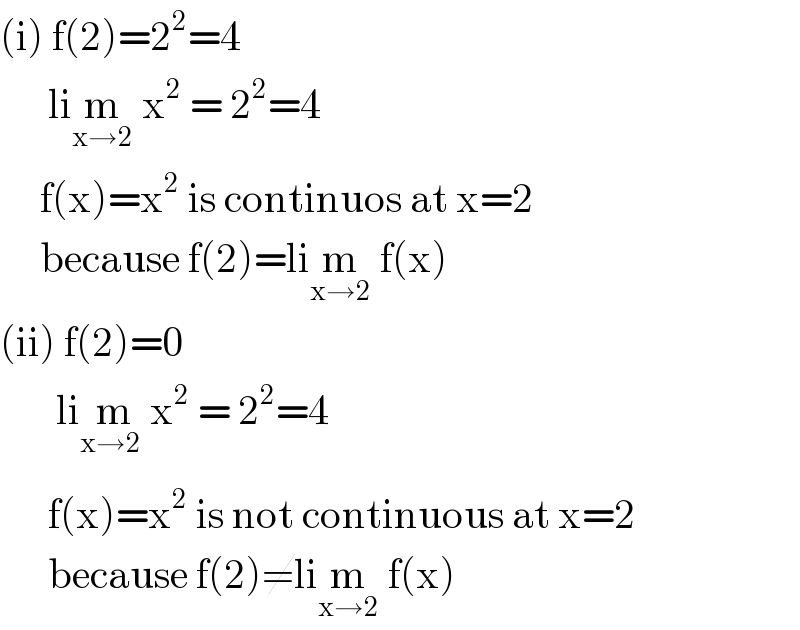
$$\left(\mathrm{i}\right)\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\:\:\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{m}}\:\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{continuos}\:\mathrm{at}\:\mathrm{x}=\mathrm{2} \\ $$$$\:\:\:\:\:\mathrm{because}\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{m}}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}_{} } {\mathrm{m}x}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{continuous}\:\mathrm{at}\:\mathrm{x}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\mathrm{because}\:\mathrm{f}\left(\mathrm{2}\right)\neq\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{m}}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$
Commented by Tawakalitu ayo mi last updated on 23/Jan/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$ \\ $$
