
Question Number 128805 by bramlexs22 last updated on 10/Jan/21
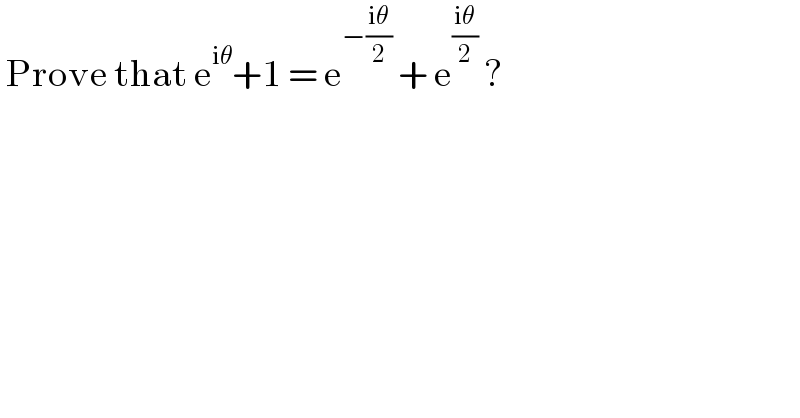
$$\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{e}^{\mathrm{i}\theta} +\mathrm{1}\:=\:\mathrm{e}^{−\frac{\mathrm{i}\theta}{\mathrm{2}}} \:+\:\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{2}}} \:? \\ $$
Commented by mr W last updated on 10/Jan/21
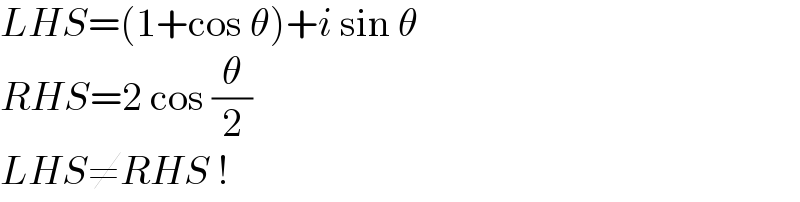
$${LHS}=\left(\mathrm{1}+\mathrm{cos}\:\theta\right)+{i}\:\mathrm{sin}\:\theta \\ $$$${RHS}=\mathrm{2}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$${LHS}\neq{RHS}\:! \\ $$
Answered by benjo_mathlover last updated on 10/Jan/21
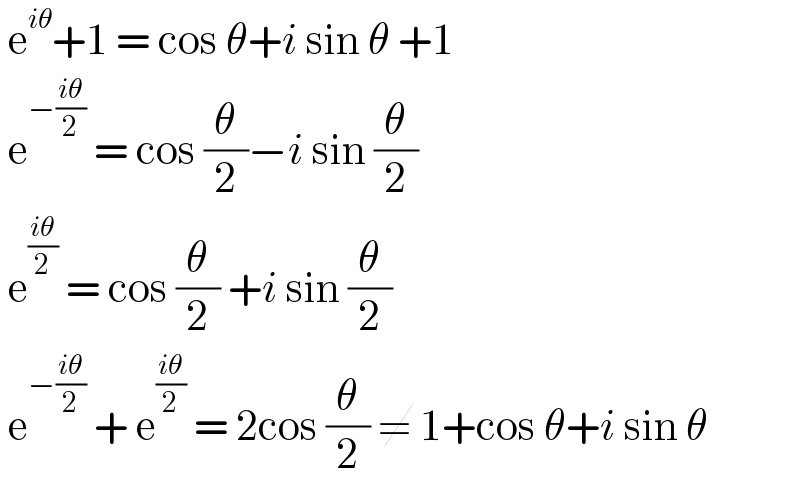
$$\:\mathrm{e}^{{i}\theta} +\mathrm{1}\:=\:\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\:+\mathrm{1} \\ $$$$\:\mathrm{e}^{−\frac{{i}\theta}{\mathrm{2}}} \:=\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−{i}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\:\mathrm{e}^{\frac{{i}\theta}{\mathrm{2}}} \:=\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\:+{i}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\: \\ $$$$\:\mathrm{e}^{−\frac{{i}\theta}{\mathrm{2}}} \:+\:\mathrm{e}^{\frac{{i}\theta}{\mathrm{2}}} \:=\:\mathrm{2cos}\:\frac{\theta}{\mathrm{2}}\:\neq\:\mathrm{1}+\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta \\ $$
