
Question Number 75208 by vishalbhardwaj last updated on 08/Dec/19
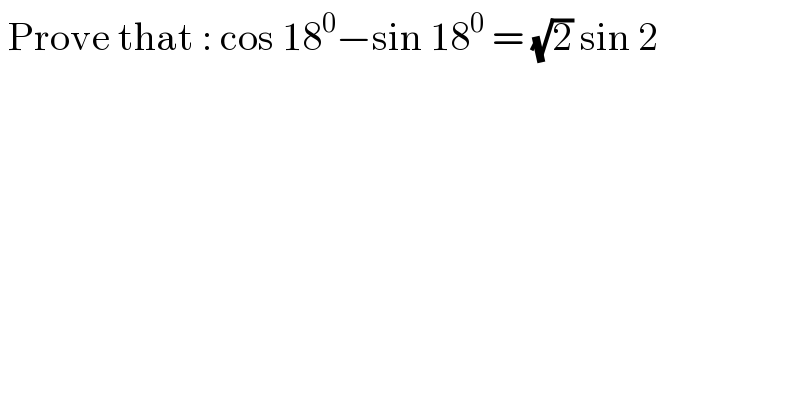
$$\:\mathrm{Prove}\:\mathrm{that}\::\:\mathrm{cos}\:\mathrm{18}^{\mathrm{0}} −\mathrm{sin}\:\mathrm{18}^{\mathrm{0}} \:=\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2} \\ $$
Answered by Kunal12588 last updated on 08/Dec/19
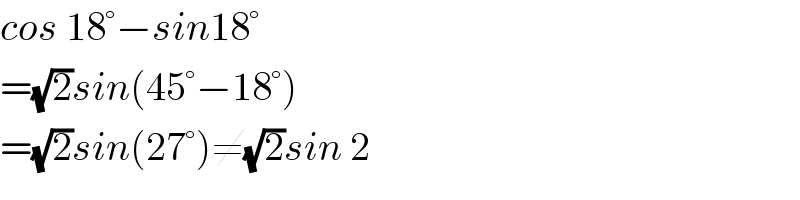
$${cos}\:\mathrm{18}°−{sin}\mathrm{18}° \\ $$$$=\sqrt{\mathrm{2}}{sin}\left(\mathrm{45}°−\mathrm{18}°\right) \\ $$$$=\sqrt{\mathrm{2}}{sin}\left(\mathrm{27}°\right)\neq\sqrt{\mathrm{2}}{sin}\:\mathrm{2} \\ $$
