
Question Number 193339 by Rajpurohith last updated on 10/Jun/23
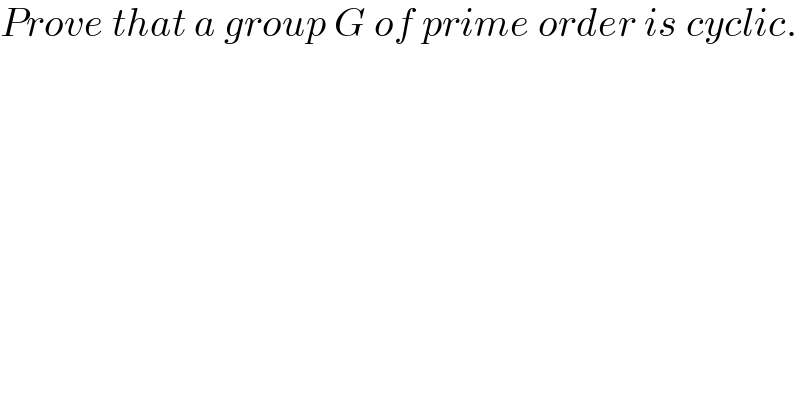
$${Prove}\:{that}\:{a}\:{group}\:{G}\:{of}\:{prime}\:{order}\:{is}\:{cyclic}. \\ $$$$ \\ $$
Answered by witcher3 last updated on 10/Jun/23

$$\mathrm{let}\:\mathrm{g}\in\mathrm{G}−\mathrm{e},\mathrm{existe}\:\mathrm{since}\:\mathrm{ord}\left(\mathrm{G}\right)=\mathrm{p}\geqslant\mathrm{2} \\ $$$$\mathrm{g}^{\mathrm{p}} =\mathrm{e} \\ $$$$\mathrm{G}\:\mathrm{contien}\:\mathrm{at}\:\mathrm{lest}\:\mathrm{2}\:\mathrm{element} \\ $$$$\mathrm{let}\:\mathrm{z}\overset{\mathrm{f}} {\rightarrow}\mathrm{G} \\ $$$$\:\:\:\:\:\:\mathrm{k}\rightarrow\mathrm{g}^{\mathrm{k}} \:\:\: \\ $$$$\mathrm{morphisme}\:\mathrm{of}\:\mathrm{Group}\: \\ $$$$\mathrm{ker}\:\mathrm{f}=\left\{\mathrm{k}\in\mathrm{Z}\:\mathrm{suche}\:\mathrm{g}^{\mathrm{k}} =\mathrm{e}\right\} \\ $$$$\Rightarrow\mathrm{p}\mid\mathrm{k}\Rightarrow\mathrm{k}=\mathrm{pm} \\ $$$$\mathrm{use}\:\mathrm{Theorem}\:\mathrm{of}\:\mathrm{morphisme}\:\mathrm{f}\:\mathrm{induce}\:\mathrm{isomorphisme} \\ $$$$\mathrm{of}\:\:\:\mathrm{Z}\swarrow\mathrm{pZ}\rightarrow\mathrm{g} \\ $$$$\Rightarrow\mathrm{g}\sim\mathrm{Z}\swarrow\mathrm{pZ}\Rightarrow\mathrm{g}\:\mathrm{Cyclic} \\ $$$$ \\ $$
Commented by Rajpurohith last updated on 11/Jun/23
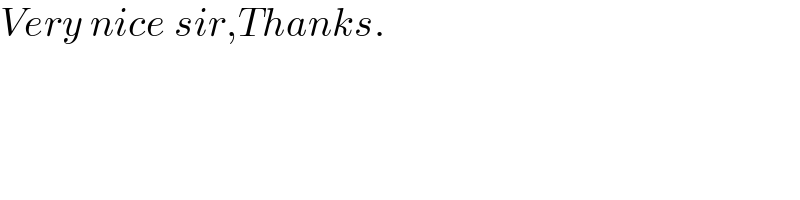
$${Very}\:{nice}\:{sir},{Thanks}. \\ $$
