
Question Number 181751 by Shrinava last updated on 29/Nov/22
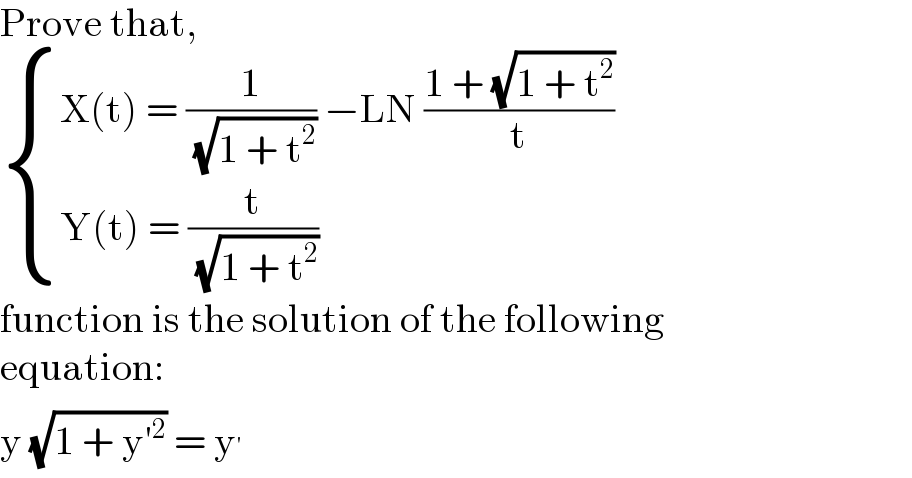
$$\mathrm{Prove}\:\mathrm{that}, \\ $$$$\begin{cases}{\mathrm{X}\left(\mathrm{t}\right)\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}\:+\:\mathrm{t}^{\mathrm{2}} }}\:−\mathrm{LN}\:\frac{\mathrm{1}\:+\:\sqrt{\mathrm{1}\:+\:\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}}}\\{\mathrm{Y}\left(\mathrm{t}\right)\:=\:\frac{\mathrm{t}}{\:\sqrt{\mathrm{1}\:+\:\mathrm{t}^{\mathrm{2}} }}}\end{cases} \\ $$$$\mathrm{function}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{equation}: \\ $$$$\mathrm{y}\:\sqrt{\mathrm{1}\:+\:\mathrm{y}'^{\mathrm{2}} }\:=\:\mathrm{y}^{'} \\ $$
