Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 206999 by efronzo1 last updated on 03/May/24

Prove that 6^(20) −1 = 0 (mod 7)

$$\:\:\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{6}^{\mathrm{20}} −\mathrm{1}\:=\:\mathrm{0}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$

Commented by Frix last updated on 03/May/24

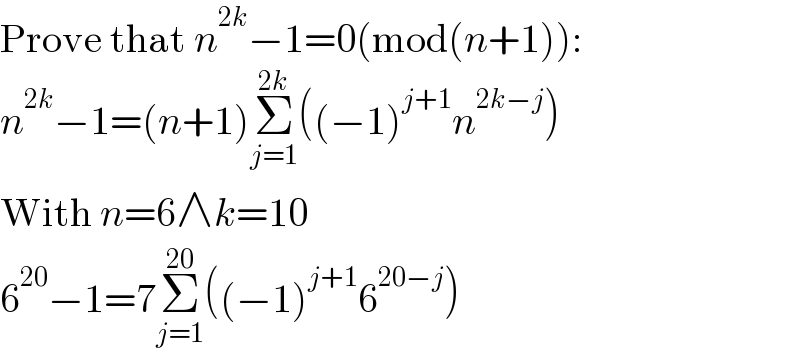
Prove that n^(2k) −1=0(mod(n+1)): n^(2k) −1=(n+1)Σ_(j=1) ^(2k) ((−1)^(j+1) n^(2k−j) ) With n=6∧k=10 6^(20) −1=7Σ_(j=1) ^(20) ((−1)^(j+1) 6^(20−j) )

$$\mathrm{Prove}\:\mathrm{that}\:{n}^{\mathrm{2}{k}} −\mathrm{1}=\mathrm{0}\left(\mathrm{mod}\left({n}+\mathrm{1}\right)\right): \\ $$$${n}^{\mathrm{2}{k}} −\mathrm{1}=\left({n}+\mathrm{1}\right)\underset{{j}=\mathrm{1}} {\overset{\mathrm{2}{k}} {\sum}}\left(\left(−\mathrm{1}\right)^{{j}+\mathrm{1}} {n}^{\mathrm{2}{k}−{j}} \right) \\ $$$$\mathrm{With}\:{n}=\mathrm{6}\wedge{k}=\mathrm{10} \\ $$$$\mathrm{6}^{\mathrm{20}} −\mathrm{1}=\mathrm{7}\underset{{j}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left(\left(−\mathrm{1}\right)^{{j}+\mathrm{1}} \mathrm{6}^{\mathrm{20}−{j}} \right) \\ $$

Answered by Rasheed.Sindhi last updated on 03/May/24

6^(20) −1≡0(mod 7) (−1)^(20) −1≡(mod 7) [∵ 6≡−1(mod 7)] 1−1≡0(mod 7) 0≡0(mod 7) Hence proved

$$\mathrm{6}^{\mathrm{20}} −\mathrm{1}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{20}} −\mathrm{1}\equiv\left({mod}\:\mathrm{7}\right)\:\left[\because\:\mathrm{6}\equiv−\mathrm{1}\left({mod}\:\mathrm{7}\right)\right] \\ $$$$\:\:\:\:\:\mathrm{1}−\mathrm{1}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{0}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\:\mathcal{H}{ence}\:{proved} \\ $$

Answered by A5T last updated on 03/May/24

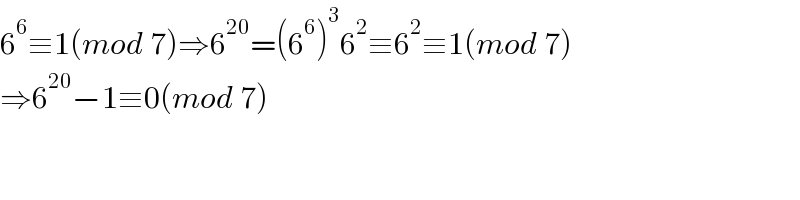
6^6 ≡1(mod 7)⇒6^(20) =(6^6 )^3 6^2 ≡6^2 ≡1(mod 7) ⇒6^(20) −1≡0(mod 7)

$$\mathrm{6}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)\Rightarrow\mathrm{6}^{\mathrm{20}} =\left(\mathrm{6}^{\mathrm{6}} \right)^{\mathrm{3}} \mathrm{6}^{\mathrm{2}} \equiv\mathrm{6}^{\mathrm{2}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\mathrm{6}^{\mathrm{20}} −\mathrm{1}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$

Answered by Rasheed.Sindhi last updated on 03/May/24

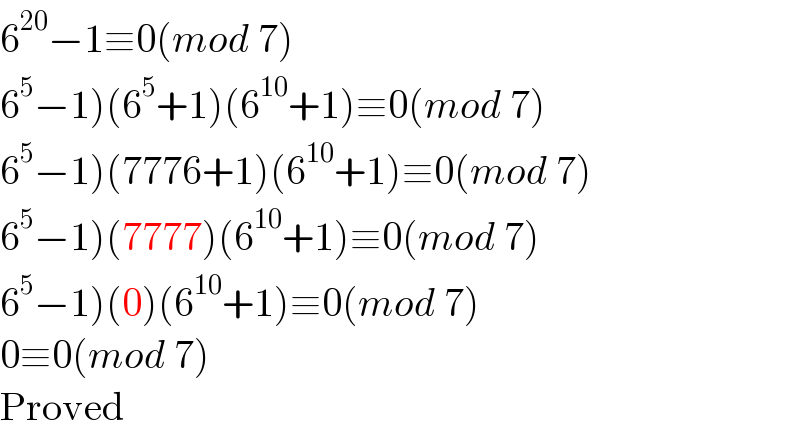
6^(20) −1≡0(mod 7) 6^5 −1)(6^5 +1)(6^(10) +1)≡0(mod 7) 6^5 −1)(7776+1)(6^(10) +1)≡0(mod 7) 6^5 −1)(7777)(6^(10) +1)≡0(mod 7) 6^5 −1)(0)(6^(10) +1)≡0(mod 7) 0≡0(mod 7) Proved

$$\mathrm{6}^{\mathrm{20}} −\mathrm{1}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\left.\mathrm{6}^{\mathrm{5}} −\mathrm{1}\right)\left(\mathrm{6}^{\mathrm{5}} +\mathrm{1}\right)\left(\mathrm{6}^{\mathrm{10}} +\mathrm{1}\right)\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\left.\mathrm{6}^{\mathrm{5}} −\mathrm{1}\right)\left(\mathrm{7776}+\mathrm{1}\right)\left(\mathrm{6}^{\mathrm{10}} +\mathrm{1}\right)\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\left.\mathrm{6}^{\mathrm{5}} −\mathrm{1}\right)\left(\mathrm{7777}\right)\left(\mathrm{6}^{\mathrm{10}} +\mathrm{1}\right)\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\left.\mathrm{6}^{\mathrm{5}} −\mathrm{1}\right)\left(\mathrm{0}\right)\left(\mathrm{6}^{\mathrm{10}} +\mathrm{1}\right)\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathrm{0}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathrm{Proved} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com